Akademik

раздел математики, в к-ром применяются топологич. понятия н методы для качественного исследования вариационных задач - существование и оценка числа экстремалей, выяснение нек-рых качественных свойств последних н соотношений между числом экстремалей различных типов. Часто в состав В. и. в ц. включают также теорию "в целом" стационарных (критических) точек функций на многообразиях, где для этих точек рассматриваются такие же задачи. (Во всяком случае, эта последняя теория тесно связана с В. и. в ц. и возникла вместе с ним, а относящиеся к ней задачи часто служат упрощенной моделью собственно вариационных задач. Иногда последние даже изучают с помощью некрой аппроксимации их первыми.) При этом интересуются всеми экстремалями (стационарными точками), существующими для данной задачи, независимо от того, отвечает ли им действительно экстремальное (т. е. минимальное или максимальное) значение рассматриваемого функционала (функции) или же это последнее является только стационарным. В этом одно из отличий В. и. в ц. от возникших ранее "классических" разделов вариационного исчисления, где после сравнительно простого вывода условии стационарности, общих для всех экстремалей, основное внимание уделялось экстремуму (хотя бы локальному), обычно минимуму. Кроме того, значительная часть "классических" разделов связана с исследованием малой окрестности экстремали, тогда как в В. и. в ц. используются топологич. свойства всего функционального пространства вариационной задачи, т. е. всего пространства кривых (функций, поверхностей н т. п.), где задан рассматриваемый функционал (или всего многообразия, где задана рассматриваемая функция).Эти свойства, в свою очередь, связываются с топологией того пространства (области, многообразия и т. д.), где должны лежать эти кривые (поверхности) или где должны быть определены и (пли) принимать значение эти функции (а также с характером краевых или еще каких-либо дополнительных условий). Такой "глобальный" характер свойственного В. и. в ц. подхода и подчеркивается в его названии определением "в целом". (В ходе развития В. и. в ц. оказалось необходимым подробнее исследовать свойства второй вариации[1], имеющей чисто локальный характер. Раньше эти свойства исследовались лишь в той мере, в какой это было нужно для применений к условиям минимума функционала.)

В. и. в ц. сложилось в 20-30-х гг. 20 в. в работах, посвященных решению задачи об оценке числа замкнутых геодезических на замкнутом римановом (более общо, финслеровом) многообразии (называемой также н е-пер и одической задачей В. и. в ц.) (см. [1]. [2]. [4]).

Общий прием исследования, свойственный для В. и. в ц., состоит в том, что для функции (в том числе и для функционала, рассматриваемого как функция на соответствующем бесконечномерном функциональном пространстве) следят за изменением тех или иных топологич. свойств области меньших значений

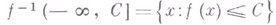
с изменением уровня функции С. Стремятся доказать, что эти свойства изменяются только при прохождении Счерез стационарные значения (отвечающие стационарным точкам функции), и описать, как связаны изменения, происходящие при таких прохождениях, со свойствами соответствующих стационарных точек.

Получаются нек-рые связи между стационарными точками , с одной стороны, и топологич. свойствами области меньших значений с достаточно большими Сили даже всего пространства, где задана ,- с другой. Если эти последние свойства известны, то из установленных связей делают определенные заключения о стационарных точках. Для собственно вариационных задач остается еще один шаг (иногда тривиальный, иногда очень трудный): полученные результаты, относящиеся к вспомогательным объектам (точки нек-рого функционального пространства), нужно интерпретировать в терминах первоначальной постановки задачи. (В задаче о замкнутых геодезических именно этот последний шаг вызывает основные затруднения.)

Описанную программу сравнительно легко удается осуществить для гладкой функции на замкнутом многообразии М. При сравнении областей меньших значений с различными Собычно используется градиентный спуск, т. е. движение точек согласно градиентной динамической системе, определяемой f и какой-нибудь вспомогательной римановой метрикой на М. Отдельно рассматривается ситуация возле стационарных точек. Если все они невырожденные, то изменение области меньших значений при прохождении Счерез стационарный уровень можно описать очень подробно - с точностью до диффеоморфизма. Такое описание, как и аналогичное описание изменений многообразий уровня 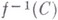, оказалось важным для топологии (см. [5], [6]), тогда как для В. и. в ц. пока оказывается достаточной менее-полная информация в терминах нек-рого числового инварианта - категории Люстерника - Шнирельмана и в терминах гомологии. Последняя приводит к Морса неравенствам, дающим обычно значительно лучшую оценку числа невырожденных критич. точек, чем категория. В то же время и оценка через категорию, и неравенства Морса годятся также без предположения о вевырожденности стационарных точек, хотя из неравенств Морса при этом следует оценка, в к-рой вырожденные стационарные точки считаются со спецпально приписываемыми им кратностямп (в связи с чем говорят об оценке числа аналитически различных стационарных точек или алгебраического числа этих точек). Категория же дает оценку числа стационарных точек в обычном смысле (подчеркивая это обстоятельство, говорят об оценке числа геометрически различных стационарных точек) и даже с нек-рой дополнительной информацией: либо число стационарных уровней не меньше , либо имеется континуум стационарных точек.

Чтобы получить аналогичные результаты для функций на бесконечномерных многообразиях, необходимы определенные дополнительные предположения об аналитич. свойствах этих функций (кроме гладкости). Наиболее полная аналогия с конечномерным случаем достигается при использовании так наз. условия (С) Пале - Смейлa (R. Palais - S. Smale, см. [7]), но оно не выполняется в нек-рых интересных случаях, а при выполнении более слабых условий соответствующие результаты тоже могут быть слабее. Затруднения может вызвать исследование траекторий градиентного спуска или какого-нибудь его аналога. Напр., для нек-рых задач геометрич. происхождения - минимальные замкнутые подмногообразия риманова многообразия, гармонические отображения - этот вопрос сводится к поведению решений параболич. систем нелинейных дифференциальных уравнений с частными производными (см. [8]). Иногда удовлетворительные результаты удается получить только для точек минимума. Основные применения - собственные значения нелинейных операторов (см. [7], [8], [9]) и многомерные задачи вариационного исчисления (т. е. такие, в к-рых рассматриваемый функционал выражается в виде некоторого кратного интеграла), в том числе упомянутые выше задачи геометрич. происхождения.

Для одномерных задач (т. е. тех, в к-рых рассматриваемый функционал выражается в виде интеграла по одной независимой переменной) вместо градиентного спуска можно использовать специфические для них более элементарные приемы [фактически с их помощью и были получены многие имеющиеся здесь результаты (см. [1], [2], [3])]. Одномерными являются задача о замкнутых геодезических и задача об оценке числа геодезич. дуг, соединяющих две точки на связном полном римановом многообразии М. Последняя полностью решена: если M не стягивается по себе в точку, то таких дуг бесконечное число (см. [10]). (На примере обычной сферы видно, что одни из этих дуг могут включать в себя многократно проходимые другие дуги.)

По-видимому, первым применением В. и. в ц. в других областях математики было вычисление гомологии классич. групп Ли (см. [11]). Важнейшим из современных применений, наряду с упомянутым выше использованием теории стационарных точек функций в топологии, является вычисление стационарных гомотопич. групп Ли (так наз. теория Ботта; см. [12]). В. и. в ц. используется также в глобальной дифференциальной геометрии (см. [13]).

Лит.-[1] Мorse М., The calculus of variations in the large, N. Y., 1934; [2] Люстерник Л. А., Шнирельман Л. Г., "Успехи матем. наук", 1947, т. 2, в. 1, с. 166-217; [3] 3ейферт Г., Трельфалль В., Вариационное исчисление в целом, пер. с нем., М., 1947; [4] Birkhoff G D "Trans. Amer. Math. Soe.", 1917, v. 18, p. 199-300; [5] Милнор Д ж., Уоллес А., Дифференциальная топология. Начальный курс, пер. с англ., М., 1972; [6] Милнор Д ж., Теорема об h-кобордизме, пер. с англ., М., 1969; [7] Иллс Д ж., "Успехи матем. наук", 1969, т. 24, № 3, с. 157-210; [8] Альбер С. И., "Успехи матем. наук", 1970, т. 25, в. 4, с. 57-122; [9] Бергер М. С., Теория бифуркаций в случае нелинейных эллиптических дифференциальных уравнений и систем, в сб.: Теория ветвления и нелинейные задачи на собственные значения, М., 1974; [10] Серр Ж. П., Сингулярные гомологии расслоенных пространств, пер. с франц., в сб.: Расслоенные пространства и их приложения, М., 1958; [11] Понтрягин Л. С., "Матем. сб.", 1939, т. 6, № 3, с. 389-422; "Успехи матем. наук", 1968Д т. 23, в. 6, с. 151-85; [12] Милнор Д ж., Теория Морса, пер. с англ., М., 1965; [13] Громол Д., Клингенберг В., Мейер В., Риманова геометрия в целом, пер. с нем., М., 1.971. Д. В. Аносов.