Akademik

- простейший конечно-разностный метод численного решения обыкновенных дифференциальных уравнений.
Пусть дано дифференциальное уравнение

с начальным условием
y(x₀) = y₀.
Выбирается достаточно малый шаг hпо оси х, строятся точки x;=x₀+ih, i=0, 1, 2, ... , и искомая интегральная кривая у(х)заменяется ломаной (ломаная Эйлера), звенья к-poй прямолинейны на отрезках [ х _i, x_i+1], а ординаты определяются по формулам

Если правая часть f(x, у )уравнения (1) непрерывна, то последовательность ломаных Эйлера при на достаточно малом отрезке равномерно стремится к искомой интегральной кривой у(х).
Э. м. заключается в том, что интеграл дифференциального уравнения (1) на каждом последовательном отрезке [ х _i, x_i+1]представляется двумя членами ряда Тейлора

На каждом шаге Э. м. имеет погрешность порядка h². Для уточнения Э. м. используются различные модификации. Напр., в усовершенствованном методе ломаных вместо формулы (2) для определения ординат используют формулу

где

то есть учитывают направление поля интегральных кривых в средней точке (4) звена ломаной.
Другой модификацией Э. м. является усовершенствованный метод Эйлера - Коши:

где

Последний метод можно еще более уточнить, применив итерационную обработку каждого значения y_i+1:

где нулевое приближение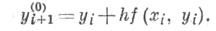

Итерационный расчет по формуле (б) продолжают до тех пор, пока два последовательных приближения не совпадут между собой в заданном числе десятичных знаков. Если после трех - четырех итераций совпадение требуемого числа десятичных знаков не достигается, то это указывает на необходимость уменьшения шага h. Э. м. с итерационной обработкой ординат дает на каждом шаге погрешность порядка h³. Э. м. и его модификации переносятся на более общий случай решения системы и обыкновенных дифференциальных уравнений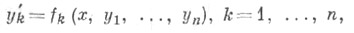
при заданных начальных условиях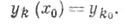
Алгоритм вычислений по Э. м. легко программируется и удобен для реализации на ЭВМ.
Метод предложен Л. Эйлером (L. Euler, 1768).

Лит.:[1] Демидович Б. П., Марон И. А., Основы вычислительной математики, М., 1960.
И. Б. Вапнярский.