Akademik

- уравнение с частными производными, имеющее вид

Здесь т - размерность пространства, с - гладкая, не равная нулю функция. В приложениях симеет смысл скорости распространения волн, а поверхности - волновых фронтов. Лучи (см. Ферма принцип )являются характеристиками Э. у.
Существует ряд обобщений и аналогов Э. у. В частности, обобщением Э. у. является уравнение

где H - однородная 1-й степени по функция, удовлетворяющая нек-рым дополнительным ограничениям. Важное значение имеет нестационарный аналог Э. у.

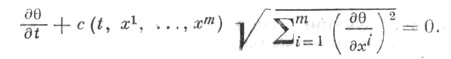
Последнее уравнение - частный случай встречающихся в теории волновых явлений дисперсионных уравнений, имеющих вид

Здесь - заданная функция.
На математич. теорию геометрич. оптики можно смотреть как на теорию Э. у. Все виды Э. у.- дифференциальные уравнения с частными производными 1-го порядка. Решение Э. у. может иметь сингулярности. Их теория - часть теории особенностей дифференцируемых отображений (см. также Гамильтона - Якоби теория, Геометрическое приближение, Лучевой метод).

Лит.: [1] Бабич В. М., Булдырев В. С., Асимптотические методы в задачах дифракции коротких воли, М., 1972; [2] Уизем Дж. Б., Линейные и нелинейные волны, пер. с англ., М., 1977.
В. М. Бабич.