Akademik

уравнение, допускающее истолкование как запись дифференциального закона развития (эволюции) во времени нек-рого процесса. Термин не имеет точного определения, и его применимость может зависеть не только от самого уравнения, но и от постановки задачи для него. Для Э. у. характерна возможность построения решения при заданном начальном условии, к-рое трактуется как запись начального состояния процесса. К Э. у. относятся, прежде всего, обыкновенные дифференциальные уравнения и их системы общего вида

и т. п. в случае, когда и(t)естественно рассматривать как решение задачи Коши; эти уравнения описывают эволюцию систем с конечным числом степеней свободы. Учет последействия приводит к интегро-дифференциальным уравнениям типа Вольтерра или к дифференциальным уравнениям с запаздывающим аргументом. Описание процессов, происходящих в сплошных средах, приводит к дифференциальным уравнениям с частными производными гиперболического, параболического и родственных типов; здесь, наряду с задачей Коши, ставится смешанная (начально-граничная) задача. Если решение .( х, t )таких уравнений трактовать как зависящий от параметра . элемент какого-либо пространства функций от х, то приходят к абстрактным дифференциальным уравнениям вида (*). Все эти уравнения, а также соответствующие им разностные уравнения и относят обычно к Э. у.
Аналогии с реальными процессами приводят к постановкам естественных задач для Э. у. (напр., задача об устойчивости решений) и порой дают методы их изучения (напр., привлечение математич. аналогов законов сохранения или диссипации полной энергии). Эволюционный характер уравнения благоприятен для его численного решения, так как значения и(r_k) (t₀<t₁<<. . .) при достаточно малом шаге можно получать с помощью постепенного перестраивания, отправляясь от начального условия. Это привело к тому, что многие задачи о стационарном состоянии среды при их численном решении трактуются как предельные при 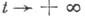для эволюционных задач. (Напр., решение уравнения Лапласа при заданных граничных условиях служит пределом решений уравнения при тех же граничных условиях и любых начальных условиях; в подобных случаях говорят об установлении решений 0. у.)
А. Д. Мышкис.