Akademik

обыкновенных дифференциальных уравнений - система обыкновенных дифференциальных уравнений, в к-рую не входит явно независимое переменное t(время). Общий вид А. с. 1-го порядка в нормальной форме:

или, в векторной записи,

Неавтономная система сводится к А. с., если ввести новую неизвестную функцию Исторически А. с. возникли при описании физич. процессов с конечным числом степеней свободы. А. с. наз. также динамическими, или консервативным и (см. Динамическая система).

Комплексная А. с. вида (1) эквивалентна вещественной А. с. с 2n неизвестными функциями

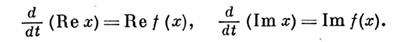
Содержательная теория комплексных А. с., отличная от вещественного случая, имеет место в случае аналитических 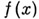(см. Аналитическая теория дифференциальных уравнений).

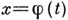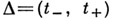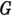Будем рассматривать А. с. с действительными коэффициентами и их действительные решения. Пусть - (произвольное) решение А. с. (1), - интервал его определения,- решение с начальными данными Пусть - область в и Точка наз. положением равновесия (точкой покоя) А. с. (1), если Положению 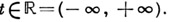равновесия отвечает решение

Локальные свойства решений.

1) Если - решение, то - решение при любом

2) Существование: при любых решение 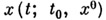существует на нек-ром интервале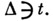

3) Гладкость: если 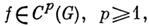то

4) Зависимость от параметров: пусть 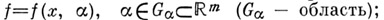если (подробнее см. [1] - [4]).

5) Пусть не является положением равновесия, тогда существуют окрестности F, Wточек 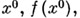соответственно, и диффеоморфизм такие, что А. с. имеет вид 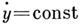в W.

Замена переменных в А. с. (1) приводит к системе

( - Якоби матрица).

Глобальные свойства решений.

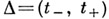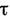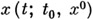1) Любое решение А. с. (1) можно продолжить на интервал . Если , то решение наз. неограниченно продолжаемым; если то решение наз. неограниченно продолжаемым "в перед повремени" (аналогично - "назад"). Если то для любого компакта существует = такое, что точка находится вне 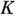при (аналогично при 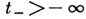; см. Продолжаемость решений дифференциальных уравнений).

2) Продолжение единственно в том смысле, что любые два решения с общими начальными данными совпадают на общей области их определения.

3) Всякое решение А. с. принадлежит к одному из трех типов: а) непериодическое, причем 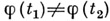для любых ) периодическое, непостоянное; с) .

Геометрическая интерпретация А. с. Каждому решению ставится в соответствие кривая Г: лежащая в области G. Тогда Gназ. фазовым пространством А. с., Г - фазовой траекторией, решение интерпретируется как движение по фазовой траектории. Фазовым потоком наз. отображение : 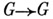по формуле 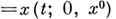(т. е. каждая точка сдвигается за время tвдоль фазовой траектории). На своей области определения фазовый поток удовлетворяет условиям: 1) непрерывно по 2) справедливо групповое свойство:

Имеет место теорема Лиувилля: пусть - область с конечным объемом, 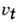- объем области тогда

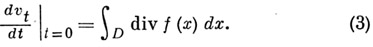
Для гамильтоновой системы из (3) следует сохранение фазового объема фазовым потоком. Другой вариант равенства (3): пусть 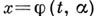- семейство решений А. с. (1), - область,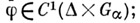 тогд

а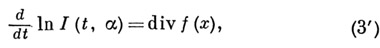

где

Структура фазовых траекторий.

1) Любые две фазовые траектории либо не имеют общих точек, либо совпадают.

2) Всякая фазовая траектория принадлежит к одному из типов: а) гладкая простая незамкнутая жорданова дуга, b) цикл, т. е. кривая, диффеоморфная окружности, с) точка (положение равновесия). Локальная структура фазовых траекторий в малой окрестности точки, отличной от положения равновесия, тривиальна (см. локальное свойство 5) решений): семейство фазовых траекторий диффеоморфно семейству параллельных прямых. Для линейной А. с. структура фазовых траекторий в окрестности положения равновесия известна, так как А. с. интегрируема (см. [5]). Для нелинейных А. с. этот вопрос принадлежит к числу не решенных до конца проблем даже при n=2 (см. Качественная теория дифференциальных уравнений). Одним из аспектов этой проблемы является вопрос об устойчивости положения равновесия (см. Устойчивости теория). Ниже приведены нек-рые результаты. Пусть - положения равновесия систем (1) и

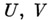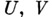- окрестности точек Системы (1) и (1') наз. эквивалентными в окрестности положения равновесия если существуют и взаимно однозначное отображение h: U->V такие, что (если т. е. при замене траектории А. с. (1) переходят в траектории А. с. 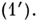Эквивалентность наз. дифференцируемой (топологической), если hесть диффеоморфизм (гомеоморфизм). Пусть - положение равновесия А. с. (1), матрица невырождена и не имеет чисто мнимых собственных значений. Тогда А. с. (1) в окрестности 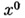топологически эквивалентна своей линейной части 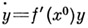. Полярный пример: А. с. где 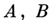- постоянные матрицы с чисто мнимыми собственными значениями и 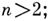неизвестно, когда эти А. с. топологически эквивалентны. Одной из самых фундаментальных задач теории А. с. является задача о структуре всего семейства фазовых траекторий. Наиболее полные результаты получены при но даже в этом случае задача далека от своего разрешения.

Лит.:[1] Петровский И. Г., Лекции по теории обыкновенных дифференциальных уравнений, 6 изд., М., 1970; [2] Понтрягин Л. С., Обыкновенные дифференциальные уравнения, 2 изд., М., 1965; [3] Коддингтон Э. А., Левинсон Н., Теория обыкновенных дифференциальных уравнений, пер. с англ., М., 1958; [4] Арнольд В. И., Обыкновенные дифференциальные уравнения, М., 1971; [5] Немыцкий В. В., Степанов В. В., Качественная теория дифференциальных уравнений, 2 изд., М.- Л., 1949.

М. В. Федорюк.