Akademik

группы G - группа всех характеров X(G) =Hom(G, А )группы Gсо значениями в абелевой группе Аотносительно операции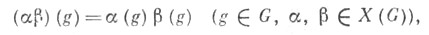

индуцированной операцией в А. В случае когда А = Т,

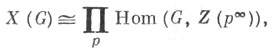
где - квазициклические группы, взятые по одной для каждого простого числа р. Эта группа алгебраически компактна (см. Сервантная подгруппа). Если при этом Gабелева, то X(G)является полной группой тогда и только тогда, когда G - группа без кручения, и редуцированной тогда и только тогда, когда Gпериодична [4].
Группа характеров топологической группы G - группа X(G)всех непрерывных гомоморфизмов 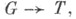снабженная компактно открытой топологией. Она является хаусдорфовой абелевой топологич. группой. Если группа Gлокально компактна, то и X(G) локально компактна, если Gкомпактна, то X(G)дискретна, а если Gдискретна, то X(G) компактна.
Примеры X. г.:

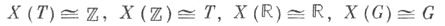
для любой конечной дискретной абелевой группы G.
С каждым непрерывным гомоморфизмом топологических групп 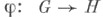связан гомоморфизм X. г. 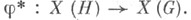При этом соответствие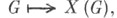 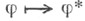ость контравариантный функтор из категории топологических групп в категорию топологических абелевых групп. Если ограничиться категорией локально компактных абелевых групп G, то этот функтор определяет эквивалентность указанной категории и двойственной к ней категории (см. Понтрягина двойственность).
Группа характеров алгебраической группы Gнад полем К - группа X(G)всех рациональных характеров Если G- абелева аффинная алгебраич. группа, то X(G)порождает пространство K[G](т. е. является базисом в этом пространстве) тогда и только тогда, когда G - диагонализируемая алгебраическая группа, т. е. изоморфна замкнутой подгруппе нек-рого тора При этом X(G) - конечно порожденная абелева группа (без р-кручения, если char K=p>0 )и К[G], является групповой алгеброй группы X(G) над К, что дает возможность определить двойственность между категорией диагонализируемых групп и категорией конечно порожденных абелевых групп (без р-кручения, если char К=р>0). В случае когда G - конечная группа (рассматриваемая как 0-мерная алгебраич. группа), эта двойственность совпадает с классич. двойственностью конечных абелевых групп.
Для любой связной алгебраич. группы G группа X(G) не имеет кручения. В частности, диагонализируемая группа G является тором тогда и только тогда, когда

Лит.:[1] Борель А., Линейные алгебраические группы, пер. с англ., М., 1972; [2] Моррис С., Двойственность Понтрягина и строение локально компактных абелевых групп, пер. с англ., М., 1980; [3] Понтрягин Л. С., Непрерывные группы, 3 изд., М., 1973; [4] Фукс Л., Бесконечные абелевы группы, пер. с англ., т. 1, М., 1974; [5] Хамфри Дж., Линейные алгебраические группы, пер. с англ., М., 1980.
А. Л. Онищик.