Akademik

- метод численного интегрирования уравнений гиперболич. типа. В гиперболич. области существует линейная комбинация исходных уравнений, в к-рую входят лишь внутренние производные вдоль характеристич. поверхностей. При этом существенно упрощаются решаемые уравнения. В X. м. решение рассчитывается на характеристич. сетке, к-рая выстраивается в процессе счета, тем самым точно учитывается область зависимости решения. Для X. м. доказаны существование решения и сходимость. Наиболее широкое применение X. м. нашел при решении задач механики сплошных сред (см. [1]). Напр., уравнения в характериотич. форме

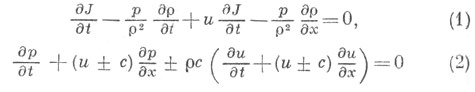
представляют собой линейную комбинацию традиционных уравнений газовой динамики: неразрывности, импульса и энергии. Здесь и ниже - плотность, и - скорость, J - внутренняя энергия единицы массы, - давление, Т - температура, х- пространственная координата, t - время. Ставится задача Коши: решение ищется в области t>0 при заданных параметрах на линии t=0. Энтропией наз. интеграл уравнения
Тогда (1) имеет вид

В левых частях (1') и (2) стоят производные взятые в направлениях

называемых характеристиками. Система (1), (2) имеет три семейства действительных характеристик. Вдоль характеристики (3) выполнено соотношение dS = 0, а вдоль характеристик (4) - соотношения

Через точку А(см. рис.) проводится характеристика (4) в сторону возрастания t

Через ближайшую к точке Асправа - точку В - проводится характеристика (4) другого семейства

С - точка пересечения характеристик. При замене выполняемых вдоль характеристик дифференциальных соотношений (5) разностными получают алгебраич. систему

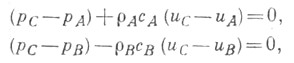
из к-рой определяются p_C и u_C. Из точки Спроводится характеристика (3)

до пересечения с линией АВ в точке D. Значение энтропии Sв точке Dопределяется путем интерполяции между точками Аи В(при этом S_C = S_D). Из уравнений

находятся значения внутренней энергии J_C и плотности 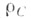в точке С. По известным данным в двух точках Аи В находится решение при большем значении времени tв точке С. Эта процедура вычислений повторяется для каждой пары точек. Затем, используя новые точки Св качестве исходных А, В, делается следующий шаг по t. Расчет проводится до необходимых величин t. Однако из-за нелинейности уравнений газовой динамики счет может прекратиться в определенный момент времени, если характеристики одного семейства будут касаться друг друга или пересекаться.
Описанная разностная схема имеет первый порядок точности (аналог метода ломаных Эйлера для решения обыкновенных дифференциальных уравнений). Повышения точности можно достигнуть путем пересчета и т. д.
X. м. можно решать стационарные многомерные задачи в области гиперболичности (для газовой динамики - сверхзвуковые течения). При этом можно определить положение вторичных ударных волн в местах, где происходит пересечение пли касание характеристик одного семейства. X. м. рассчитываются задачи с небольшим числом разрывов, так как при скоплении особенностей вычисления затруднены. Расчет X. м. состоит из ряда элементарных задач: расчет внутренней точки, точек на ударной волне или на обтекаемом теле и т. п.
Возможно построение численных схем X. м., позволяющих вести счет по лслоям