Akademik

- мероморфная функция в ограниченной области Dкомплексного пространства , удовлетворяющая относительно некоторой дискретной группы , действующей в этой области, уравнению:

где - якобиан отображения a m- целое число, наз. весом автоморфной формы. Если группа Г действует без неподвижных точек, то А. ф. определяют дифференциальные формы на фактор-пространстве и обратно. С помощью А. ф. можно строить нетривиальные автоморфные функции. Оказывается, что если - голоморфная и ограниченная в области 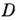функция, то ряд

сходится при больших m, давая тем самым нетривиальную А. ф. веса m. Эти ряды наз. тета-рядами Пуанкаре.

Приведенное выше классич. определение А. ф. послужило в последнее время исходным пунктом для весьма широкого обобщения этого понятия в теории дискретных подгрупп групп Ли и групп аделей (см.[3]).

Лит.:[1] Пуанкаре А., Избр. труды, т. 3, пер. с франц., М., 1974; [2] 3игель К. Д., Автоморфные функции нескольких комплексных переменных, пер. с англ., М., 1954; [3] Арифметические группы и автоморфные функции, пер. с англ, и франц., М., 1969. А. Н. Паршин.