Akademik

объекта категории - понятие, частным случаем к-рого являются понятия фактормножества, факторгруппы, факторпространства и т. п.
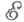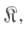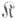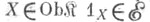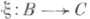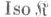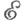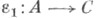Пусть -нек-рый класс эпиморфизмов категории содержащий все тождественные морфизмы из и выдерживающий умножение справа на изоморфизмы. Другими словами, для любого и для всякого из и всякого из морфизм Морфизмы и из 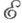наз. эквивалентными, если 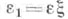для нек-рого изоморфизма 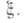Класс эквивалентности морфизма 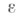наз. -факторобъектом объекта А, а пара 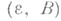-представителем этого Ф. Факторобъект с представителем 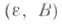иногда обозначается
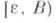или просто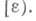
Для каждого объекта Акласс всех его 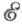-факторобъектов непуст; в нем имеется несобственный Ф. [1_A, L), остальные 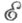-факторобъекты этого класса собственные. Категория 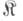наз. 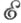-локально малой справа, если для каждого объекта Аиз 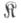класс 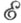-факторобъектов является множеством.
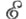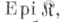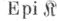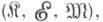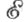Если в качестве взять подкатегорию всех эпиморфизмов то -факторобъекты наз. просто факторобъектами. Если в категории имеется бикатегорная структура то -факторобъекты наз. допустимыми Ф. Аналогично, если 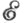состоит из всех регулярных (строгих, нормальных и т. п.) эпиморфизмов, то соответствующие Ф. наз. регулярными (нормальными, строгими и т п.). Напр.. в категории топологич. пространств факторпространства соответствуют регулярным Ф.
Понятие Ф. объекта категории дуально понятию подобъекта объекта категории.

М. Ш. Цаленко.