Akademik

локально выпуклое линейное топология, пространство, обладающее рядом свойств банаховых пространств и Фреше пространств без предположения о метризуемости; это один из наиболее широких классов пространств, в к-рых справедлива Банаха - Штейнхауза теорема. Б. п. были впервые введены Н. Бурбаки (см. [1]).

Множество Авекторного пространства Еназ. уравновешенным множеством, если для всех , для к-рого . Множество 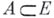наз. поглощающим множеством, если оно поглощает каждую точку из Е, т. е. если для каждого существует такое , что .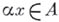

Бочкой в линейном топологич. пространстве наз. замкнутое, уравновешенное поглощающее выпуклое множество. Бочечным пространством наз. линейное топологич. пространство, наделенное локально выпуклой топологией, в к-рой всякая бочка является окрестностью нуля. Пространства Фреше и, в частности, банаховы пространства служат примерами Б. п. Важный класс Б. п., наделенных особенно замечательными свойствами, составляют Монтеля пространства.

Свойства Б. п. Фактор пространство, прямая сумма и индуктивный предел Б. п. являются Б. п. Всякое поточечно ограниченное множество линейных непрерывных изображений Б. п.-в локально выпуклое линейное топологич. пространство равностепенно непрерывно. В пространстве, сопряженном к Б. п., ограниченное множество в слабой топологии будет ограниченным в сильной топологии и компактным в слабой топологии. Замкнутая выпуклая оболочка компактного множества, лежащего в пространстве, сопряженном к Б. п., компактна.

Лит.:[1] Бурбаки Н., Топологические векторные пространства, пер. с франц., М., 1959; [2] Эдварде Р., Функциональный анализ, пер. с англ., М., 1969. В. М. Тихомиров.