Akademik

приближающей функции-расстояние r (g, f) между приближающей функцией 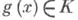и заданной функцией В одном и том же классе 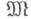могут рассматриваться различные метрики 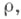напр. равномерная метрика

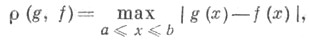
интегральные метрики

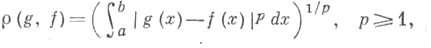
и др. В качестве класса Кприближающих функций рассматриваются алгебраич. многочлены, тригонометрич. полиномы, а также множества частичных сумм ортогональных разложений функции f(х) по ортонормированным системам, линейные средние этих частичных сумм и целый ряд др. множеств.

Лит.:[1] Чебышев П. Л., Полн. собр. соч., т. 2, М.- Л., 1947; [2] Натансон И. П., Конструктивная теория функций, М.- Л., 1949; [3] Гончаров В. Л., Теория интерполирования и приближения функций, 2 изд., М., 1954; [4] Ахиезер Н. И., Лекции по теории аппроксимации, 2 изд., М., 1965; [5] Никольский С. М., Приближение функций многих переменных и теоремы вложения, М., 1969.
А. В. Ефимов.