Akademik

кольцо R, являющееся топологич. пространством, причем требуется, чтобы отображения

были непрерывны. Т. к. Rназ. отделимым, если оно отделимо как топологич. пространство. В этом случае пространство R хаусдорфово. Любое подкольцо МТ. к. R, а также факторкольцо R/J по идеалу J являются Т. к. Если Rотделимо и идеал J замкнут, то R/J - отделимое Т. к. Замыкание подкольца Мв Rтакже является Т. к. Прямое произведение топологич. колец - Т. к.
Гомоморфизм топологич. колец - это гомоморфизм колец, являющийся непрерывным отображением. Если 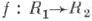- такой гомоморфизм, причем f- эпиморфизм и открытое отображение, то R₂ как Т. к. изоморфно кольцу R₁/Ker f. Примеры Т. к. доставляют банаховы алгебры. Важный тип Т. к. определяется тем условием, что в качестве фундаментальной системы окрестностей нуля можно выбрать некоторое множество идеалов. Например, с любым идеалом коммутативного кольца Rсвязана -адическая топология, в к-рой множества для всех натуральных побразуют фундаментальную систему окрестностей нуля. Эта топология отделима, если выполнено условие

Для Т. к. Rопределено его пополнение являющееся полным Т. к., причем отделимое кольцо Rвкладывается в к-рое тоже отделимо, как всюду плотное подмножество. Аддитивная группа кольца совпадает с пополнением аддитивной группы кольца Rкак абелевой топологич. группы.

Лит.:[1] Бурбаки Н., Общая топология. Топологические группы. Числа и связанные с ними группы и пространства, пер. с франц., М., 1969; [2] его же, Коммутативная алгебра, пер. с франц., М., 1971; [3] Понтрягин Л. С., Непрерывные группы, 3 изд., М., 1973; [4] Ван дер Варден Б. Л., Алгебра, пер. с нем., 2 изд., М., 1979.
Л. В. Кузьмин.