Akademik

над топологическим полем (т. п.), К - векторное пространство Енад К, наделенное топологией, согласующейся со структурой векторного пространства, т. е. удовлетворяющей следующим аксиомам: 1) отображение непрерывно; 2) отображение непрерывно (при этом предполагается, что произведения и наделены произведениями соответствующих топологий). Совершенно аналогично можно определить топологическое левое и правое векторные пространства над (не обязательно коммутативным) топологич. телом. Для обозначения Т. в. и. Ес топологией 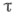иногда будет использоваться символ с другой стороны, упоминание о поле Кчасто будет опускаться.
Т. в. п. Е ₁ и Е ₂ над одним и тем же т. п. наз. изоморфными, если существует непрерывное линейное взаимно однозначное отображение Е ₁ на Е ₂. обратное к к-рому также непрерывно. Размерностью Т. в. п. наз. размерность векторного пространства Е.

Способы задания топологии Т. в. п. и ее свойства. Пусть - Т. в. п. над т. п. К. Топология 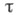инвариантна относительно сдвигов (т. е. для каждого отображение представляет собой гомеоморфизм Ена себя); поэтому топология однозначно определяется базой (базисом, фундаментальной системой) окрестностей всякой фиксированной точки (в частности, нуля). Топология согласуется со структурой аддитивной группы пространства Е, и справедливы следующие предложения. 1. Для того чтобы Ебыло отделимым, необходимо и достаточно, чтобы для всякой точки существовала окрестность нуля, не содержащая х.2. Если . отделимо, то оно вполне регулярно. 3. В E существует единственная равномерная структура, обладающая следующими свойствами: а) она инвариантна относительно сдвигов (т. е. для нее все сдвиги представляют собой равномерно непрерывные отображения); б) ассоциированная с ней топология совпадает с исходной топологией пространства Е. Множество в Т. в. п. наз. полным, если оно полно относительно равномерной структуры, о к-рой только что шла речь. Т. о., Т. в. п. Еполно, если всякий Коши фильтр в Есходится. Для всякого Т. в. п. Есуществует полное Т. в. п. над тем же полем, содержащее Ев качестве всюду плотного подмножества и индуцирующее на Еисходные линейную структуру и топологию; оно наз. пополнением пространства Е. Всякое отделимое Т. в. п. обладает отделимым пополнением, единственным с точностью до изоморфизма, оставляющего неподвижными элементы пространства Е. Всюду далее предполагается, если не оговорено противное, что К - недискретное нормированное поле, наделенное топологией, определяемой нормой. Если Е - векторное пространство над К, то множество называется закругленным (или уравновешенным), если при 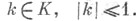Если . и В- два подмножества в Е, то говорят, что А поглощает В, если существует такое положительное число r, что при Подмножество пространства Еназ. поглощающим (или радиальным), если оно поглощает каждое одноточечное множество. Во всяком Т. в. п. Енад . существует база замкнутых окрестностей нуля со следующими свойствами: 1) для всякого множества 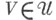существует такое, что 2) каждое - закругленное поглощающее множество; 3) если то и для всякого С другой стороны, пусть - топология в векторном пространстве Енад К, инвариантная относительно сдвигов и обладающая базой окрестностей нуля, имеющей свойства (1) и (2), а также следующее свойство: За) существует такое что, если то и Тогда Е, наделенное топологией -Т. в. п. над K (в том случае, когда норма в поле Кархимедова, (За) является следствием остальных требований, наложенных на Всякий базис фильтра в векторном пространстве Енад К, обладающий свойствами (1), (2), (За), а в случае поля с архимедовой нормой - хотя бы свойствами (1) и (2),- является фундаментальной системой окрестностей нуля (не обязательно замкнутых) нек-рой однозначно определяемой топологии в Е, согласующейся со структурой векторного пространства в Е. Т. в. п. Енад полем вещественных чисел или над полем комплексных чисел и его топология наз. локально выпуклыми, если Еобладает базой окрестностей нуля, состоящей из выпуклых множеств (иногда в определение локально выпуклого пространства включается еще требование его отделимости).

Примеры. 1. Всякое т. п. Кможет рассматриваться как (одномерное) Т. в. п. над К;рассматриваемое таким образом, оно будет обозначаться символомК ₀;
2. Пусть I - нек-рое непустое множество и - векторное пространство над К, представляющее собой произведение I экземпляров векторного пространства К ₀,наделенное топологией, являющейся произведением топологий сомножителей. Тогда - Т. в. п.
3. Если топология т. п. Кдискретна, то всякое векторное пространство Енад К, наделенное топологией, согласующейся со структурой ого аддитивной группы и инвариантной относительно операций умножения на ненулевые элементы из К, является Т. в. п. (этим условиям удовлетворяет, в частности, дискретная топология в Е). Т. в. п. над полями с дискретной топологией наз. топологическими векторными группами.
4. Пусть Е - векторное пространство над т. п. К, - нек-рое множество полунорм на Е. Шаром радиуса r>0 по полунорме р на Еназ. множество Множество пересечений всевозможных конечных семейств шаров [всевозможных (положительных) радиусов] по (всевозможным) полунормам, принадлежащим множеству образует базис окрестностей нуля нек-рой топологии в Е, согласующейся со структурой векторного пространства; говорят, что эта топология задастся, или определяется семейством полунорм Если К= или то топология локально выпукла; обратно, топология всякого локально выпуклого пространства (л. в. п.) Еможет бытьзадана нок-рым множеством полунорм - например, множеством калибровочных функций (функционалов Минковского) произвольной предбазы окрестностей нуля в Е, состоящей из закругленных выпуклых множеств.
Подмножество Т. в. п. наз. ограниченным, если оно поглощается всякой окрестностью нуля.
Т. в. п. наз. нормируемым, если его топология может быть задана одной нормой. Для того чтобы Т. в. п. над полем 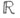или было нормируемым, необходимо и достаточно, чтобы оно было отделимым и обладало выпуклой ограниченной окрестностью нуля (теорема Колмогорова).
5. Пусть п - натуральное число, I_n - множество, содержащее пэлементов и Топология в определяется нормой где символ 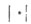обозначает норму в К. Если поле Кполно, то всякое п- мерное Т. в. п. над Кизоморфно пространству (при n=1 это верно и без предположения полноты K). Если поле . локально компактно, то для того, чтобы отделимое Т. в. п. над . было конечномерным, необходимо и достаточно, чтобы оно обладало предкомпакт-ной окрестностью нуля (теорема Тихонова). Т. в. п. наз. метризуемым, если его топология может быть задана нек-рой метрикой (среди таких метрик всегда существует метрика, инвариантная относительно сдвигов). Для метризуемости Т. в. п. необходимо и достаточно, чтобы оно было отделимым и обладало счетной базой окрестностей нуля.
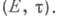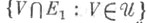6. Пусть - Т. в. п., E₁ - векторное подпространство векторного пространства - топология, индуцированная в E₁ топологией Е. Топология согласуется со структурой векторного пространства E₁; Т. в. п. наз. топологическим векторным подпространством Т. в. п. Если - база (соответственно, предбаза) окрестностей нуля в то множество образует базу (соответственно, предбазу) окрестностей нуля в Если отделимо (cоответственно, метризуемо, локально выпукло), то и таково же. Если топология задается нек-рым множеством полунорм, то топология определяется сужениями этих полунорм на E₁.
7. Пусть и E₁ -те же, что в предыдущем пункте, и - факторпространство векторного пространства Епо его подпространству E₁. Фактортопология в согласуется со структурой векторного пространства в Т. в. п. наз. топологическим векторным факторпространство м Т. в. п. по E₁. (По определению фактортопологии, множество 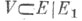открыто в в точности тогда, когда его прообраз относительно канонич. отображения открыт в Если - база окрестностей нуля в Е, то множество образов ее элементов относительно канонич. отображения образуют базу окрестностей нуля в (для предбаз это, вообще говоря, не так). Для того чтобы Т. в. п. 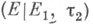было отделимым, необходимо и достаточно, чтобы подпространство E₁ было замкнуто в Если -замыкание одноточечного множества {0} в то (отделимое) топологич. векторное факторпространство 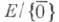наз. отделимым Т. в. п., ассоциированным с Т. в. п. Е;конечно, если само Еотделимо, то ассоциированное с ним отделимое Т. в. п. ему изоморфно. Если Елокально выпукло (соответственно, если . метризуемо, a E₁ замкнуто; если Еметризуемо и полно), то локально выпукло (соответственно, метризуемо; полно); однако Еможет быть полным (неметризуемым) без того, чтобы (даже отделимое и метризуемое) его топологическое векторное факторпространство было полно (см. ниже).
8. Пусть 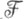- векторное пространство всех измеримых по Лебегу действительных функций на - мера Лебега на этом отрезке и для каждого

Множество образует базис фильтра в 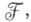обладающий (определенными выше) свойствами (1) и (2); пусть - согласующаяся со структурой векторного пространства топология в для к-рой является базой окрестностей нуля, и - ассоциированное с отделимое Т. в. п. (само неотделимо). Т. в. п. метризуемо, но не локально выпукло; его можно отождествить - как векторное пространство - с пространством классов -эквивалентных -измеримых действительных функций на [0, 1]; сходимость последовательностей в пространстве (соответственно, в пространстве совпадает со сходимостью по мере (в первом случае - индивидуальных функций, а во втором - классов -эквивалентности таких функций).
Всюду далее предполагается, что или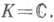
9. Пусть - векторное пространство всех бесконечно дифференцируемых функций 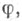определенных на принимающих значения в Ки удовлетворяющих следующему условию 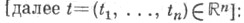для всех

где

Наделенное топологией задаваемой семейством норм p_rk,определяемых предыдущим равенством, Sстановится полным метризуемым локально выпуклым пространством (такие пространства наз. пространствами Фреше). Пространство играет важную роль в теории обобщенных функций. Интересно, что на . не существует никакой нормы, превращающей S в банахово пространство, в топологии к-рого каждая из функций непрерывна (в частности, л. в. п. ненормируемо).
Некоторые методы построения Т. в. п.
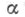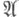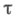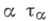1. Проективные топологии. Пусть Е - векторное пространство и для каждого из нек-рого множества индексов - линейное отображение Ев Т. в. п. тогда в Есреди всех топологий, для к-рых непрерывны все отображения существует самая слабая топология (она является верхней гранью семейства топологий где для каждого - топология в Топология наз. 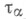проективной топологией - а наделенное ею пространство Е - проективным пределом семейства пространств относительно отображений топология согласуется со структурой векторного пространства в Е, а если все пространства Елокально выпуклы, то таково же и (Иногда термин лпроективный предел