Akademik

разрешимое многообразие,- однородное пространство Мсвязной разрешимой группы Ли G; его можно отождествить с пространством смежных классов G/H, где Н - стационарная подгруппа нек-рой точки многообразия М.
IIримеры: тор Т ⁿ, многообразие Ивасавы N/l (где N - группа всех верхних треугольных матриц с единицами на диагонали в I - подгруппа всех целых точек в N), К ² (бутылка Клейна), Mb (лист Мёбиуса).
Первым среди С. был изучен более узкий класс нильмногообразий, т. е. однородных пространств нильпотентных групп Ли (таковы 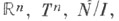а К ² и Mb нильмногообразиями не являются). Для них А. И. Мальцевым были доказаны следующие утверждения (см. [5]). 1) Всякое нильмногообразие M = G/H диффеоморфно где М*- компактное нильмногообразие. 2) Если Мкомпактно и действие G на Мэффективно, то стационарная подгруппа H является дискретной подгруппой.3) Нильпотентная группа Ли . может транзитивно и локально эффективно действовать на нек-ром компактном многообразии тогда и только тогда, когда ее алгебра Ли имеет -форму. При этом если Gодносвязна, то она изоморфна унипотентной алгебраич. группе, определенной над и Нявляется арифметич. подгруппой в G.4) Фундаментальная группа компактного нильмногообразия М(изоморфная Н, если Gодносвязна и ее действие на Млокально эффективно) определяет его однозначно с точностью до диффеоморфизма. Фигурирующие здесь группы - это в точности всевозможные конечно порожденные нильпотентные группы без кручения. Эти результаты отчасти обобщаются на произвольные С. Так, для произвольного С. Мсуществует С. М', конечнолистно накрывающее его и диффеоморфное где М* - нек-рое компактное С. Произвольное С. не всегда разлагается в прямое произведение но диффеоморфно (см. [1], [4]) пространству векторного расслоения над нек-рым компактным С. (для Mb соответствующим расслоением является нетривиальное линейное расслоение над S¹). Фундаментальная группа произвольного С. Мполициклична и, если Мкомпактно, определяет многообразие однозначно с точностью до диффеоморфизма. Группа изоморфна для нек-рого компактного С. Мтогда и только тогда, когда она включается в точную последовательность вида

где - нек-рая конечно порожденная нильпотентная группа без кручения. В каждой полициклич. группе существует подгруппа конечного индекса, изоморфная для нек-рого компактного С. М. Если разрешимая группа Ли Gдействует на компактном С. M=GlH транзитивно и локально эффективно, то . расслаивается над тором со слоем где N - нильрадикал в С. Компактность С. M=G/Н эквивалентна наличию на MG- инвариантной меры, относительно к-рой объем Мконечен.
Каждое С. Масферично (т. с. гомотопич. группы при Среди всех компактных однородных пространств компактные С. характеризуются асферичностью и разрешимостью группы (см. [3]).

Лит.:[1] Auslander L., лBull. Amer. Math. Soc.