к-рый переводится данным оператором в пропорциональный ему вектор, т. е. 
Коэффициент
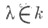наз. собственным значением оператора А. Если оператор А линеен, то множество
всех С. в., отвечающих собственному значению 
вместе с нулевым вектором, является линейным подпространством. Оно наз. собственным подпространством оператора А, отвечающим собственному значению 
и совпадает с ядром 
оператора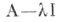 
(т. е. с множеством векторов, переводимых этим оператором в 0). Если L - топологич. векторное пространство и А - непрерывный оператор, то 
замкнуто для любого 
Вообще говоря, собственное подпространство не обязано быть конечномерным, но если А вполне непрерывен (компактен), то 
конечномерно для любого ненулевого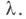 
В сущности, наличие С. в. у операторов в бесконечномерных пространствах - явление довольно редкое, хотя важные для приложений операторы специальных классов (интегральные, дифференциальные и т. п.) часто обладают обширными наборами С. в.
Обобщением понятий С. в. и собственного подпространства являются понятия корневого вектора и корневого подпространства. У нормальных (в частности, самосопряженных или унитарных) операторов все корневые векторы являются собственными, и собственные подпространства, отвечающие различным С. в., взаимно ортогональны.
Лит.:[1] Иосида К., Функциональный анализ, пер. с англ., М., 1967; [2] Люстерник Л. А., Соболев В. Н , Элементы функционального анализа, 2 изд., М., 1965; [3] Канторович Л. В., Акилов Г. П., Функциональный анализ, 2 изд., М., 1977.
Т. С. Пиголкина, В. С. Шулъман.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.