Akademik

полугруппа с единицей и с двумя образующими 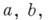заданная определяющим соотношением . Одна из реализаций Б. п.- декартов квадрат , где - множество неотрицательных целых чисел относительно операции

Б. п. является инверсной полугруппой и как инверсная полугруппа моногенна, т. е. порождена одним элементом. Идемпотенты Б. п. образуют цепь, упорядоченную по типу неотрицательных чисел. Б. п. бипроста (см. Простая полугруппа).

Б. п. нередко возникают в теоретико-полугрупповых исследованиях, не только как один из представителей нек-рых важных классов полугрупп, но и в качестве "блоков", определяющих строение тех или иных полугрупп. Напр., для всякого идемпотента е0-простой, но не вполне 0-простой полугруппы Sсуществует бициклическая подполугруппа в S, содержащая е в качестве единицы (см. [1], 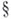2. 7). Указанные в определении элементы аи b Б. п. В будут соответственно ее левым и правым увеличительными элементами (т. е. существуют такие собственные подмножества Xи Y в В, что 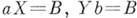). Более того, в полугруппе Sс единицей еэлемент сбудет левым увеличительным тогда п только тогда, когда Sсодержит бици-клическую полугруппу, единица к-рой совпадает с e, а роль элемента аиграет с; аналогичное утверждение верно для правых увеличительных элементов, так что Sобладает левыми увеличительными элементами тогда и только тогда, когда она обладает правыми увеличительными элементами.

Лит.:[1] Клиффорд А., Престон Г., Алгебраическая теория полугрупп, пер. с англ., т. 1-2, М., 1972; [2] Ляпин Е. С., Полугруппы, М., 1960. Л. Н. Шеврин.