дифференциального уравнения
(*)
в области D - локально интегрируемая функция и, удовлетворяющая равенству
для любой гладкой (напр., класса 
) функция j с компактным носителем в D. Здесь коэффициенты а a (х).уравнения (*) предполагаются достаточно гладкими и L* означает формально сопряженный по Лагранжу с Lдифференциальный оператор
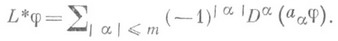
Напр., обобщенную производную f=Dauможно определить как такую локально интегрируемую функцию f, что иесть С. р. уравнения Dau=f.
При рассмотрении С. р. уравнения (*) возникает задача: при каких условиях они являются сильными решениями. Напр., для эллиптич. уравнений всякое С. р. является сильным.
Лит.:[1] Бицадзе А. В., Некоторые классы уравнений в частных производных, М., 1981. А. П. Солдатов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.