Akademik

степенной ряд вида

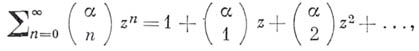
где - целое, а - произвольное фиксированное число (вообще говоря, комплексное), 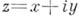-. комплексное переменное, - биномиальные коэффициенты. Для целых 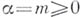Б. р. сводится к конечной сумме 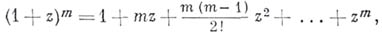слагаемых называемой Ньютона биномом. Для остальных значений 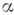Б. р. абсолютно сходится при и расходится при 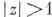.В граничных точках единичной окружности 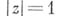Б. р. ведет себя следующим образом: 1) если 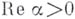, то он абсолютно сходится во всех точках окружности 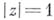; 2) если 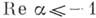, то он расходится во всех точках окружности ; 3) если 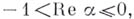то Б. р. расходится в точке и условно сходится во всех остальных точках окружности 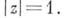Во всех точках, в к-рых Б. р. сходится, он представляет главное значение функции , равное 1 при 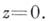Б. р. является частным случаем гипергеометрического ряда.

Если - действительные числа, причем а не есть целое неотрицательное число, то Б. р. ведет себя следующим образом: 1) если , то он абсолютно сходится при 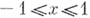; 2) если 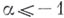, то Б. р. абсолютно сходится при и расходится при всех иных значениях х;3) если , то Б. р. абсолютно сходится при 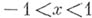, условно сходится при 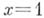и расходится 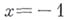при ; при 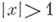Б. р. всегда расходится.

Б. р. появляется впервые, по-видимому, у И. Ньютона (I. Newton) в 1664-65. Исчерпывающее исследование Б. р. было проделано Н. Абелем [1]. Оно послужило началом теории степенных рядов в комплексной области.

Лит.:[1] Abel N.. "J. reine und angew. Math.", 1826, Bd 1, № 4; S. 311-39; [2] Knopp K., Theorie und Anwendung dcr unendlichen Rcihen, 5 Aufl., В., 1947; [3] Маркушевич А. И., Теория аналитических функций, 2 изр., т. 1, М. 1967. Е. Д. Соломенцев