Akademik

-преобразования полугрупп, удовлетворяющие специальным условиям: правым сдвигом полугруппы S наз. преобразование r такое, что дли любых 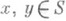имеет место ( ху)r=х(yr); левый сдвиг определяется симметричным образом, при этом ради удобства левые сдвиги чаще записывают как левые операторы. Таким образом, л е в ы й с д в и г полугруппы S - такое ее преобразование l, что для любых 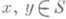имеет место l( ху) =(lх) у. Соответственно последовательность выполнения двух левых сдвигов в произведении (см. Преобразований полугруппа )осуществляется справа налево. Произведение двух левых (правых) С. п. само будет левым (правым) С. п., так что множество 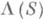(соответственно Р(S))всех левых (правых) С. п. Sбудет подполугруппой симметрич. полугруппы . Для произвольного элемента преобразование l_a(r_a), заданное формулой является левым (правым) сдвигом, соответствующим элементу а. Он наз. в н у т р е н н и м л е в ы м (п р а в ы м) с д в и г о м. Множество 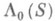(соответственно P₀(S))всех внутренних левых (правых) С. п. Sесть левый идеал в (правый идеал в Р(S)).

Левый сдвиг lи правый сдвиг r полугруппы Sназ. с в я з а н н ы м и, если х(lу)=(хr)удля любых х, ;в этом случае пару (l,r) наз. б и с д в и г о м S. Для любого пара (l _а, r _а) есть бисдвиг; он наз. в н у т р е н н и м б и с д в и г о м, соответствующим элементу а. Вполугруппах с единицей и только в них всякий бисдвиг внутренний. Множество Т(S)всех бисдвигов полугруппы Sесть подполугруппа декартова произведения 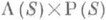; она наз. сдвиговой оболочкой полугруппы S. Множество Т ₀ (S)всех внутренних бисдвигов есть идеал в Т (S);он наз. в н у т р е н н е й ч а с т ь ю Т(S). 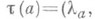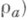Отображение , заданное формулой , есть гомоморфизм Sна Т ₀(S), называемый каноническим. Полугруппа Sназ. слабо редуктивной, если для любых из того, что ах=bх и ха=хb для всех , следует а=b;т. е. канонич. гомоморфизм полугруппы Sесть изоморфизм. Если Sслабо редуктивна, то Т (S)совпадает с идеализатором Т ₀ (S)в , т. е. с наибольшей подполугруппой из , содержащей Т ₀(S) в качестве идеала.

С. п. и, в частности, сдвиговые оболочки играют существенную роль при изучении идеальных расширений полугрупп. Роль сдвиговой оболочки при этом в известной степени аналогична роли голоморфа группы в теории групп.

Лит.:[1] К л и ф ф о р д А., П р е с т о н Г., Алгебраическая теория полугрупп, пер. с англ., т. 1, М., 1972; [2] P e t r i c h М., Introduction to semigroups. Columbus, Ohio, 1973; [3] е г о ж е, "Semigroup Forum", 1970, v. 1, p. 283-360.

Л. Н. Шеврин.