Akademik

г р у п п ы G - наибольшее связное подмножество G° топологической (или алгебраической) группы G, содержащее единицу этой группы. С. к. е. G^o является замкнутой нормальной подгруппой в G; смежные классы по этой подгруппе совпадают со связными компонентами группы G. Факторгруппа G/G° вполне несвязна и хаусдорфова, причем G° - наименьшая из таких нормальных подгрупп , что G/Hвполне несвязна. Если Gлокально связна (напр., G - группа Ли), то G^o открыта в G и G/G° дискретна.

В произвольной алгебраич. группе GС. к. е. G° также открыта и имеет конечный индекс, причем G°является минимальной замкнутой подгруппой конечного индекса в G. Связные компоненты алгебраич. группы Gсовпадают с неприводимыми компонентами. Для любого регулярного гомоморфизма 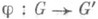алгебраич. групп справедливо равенство j(G°) = j(G)°. Если G определена над нек-рьш полем k, то и G° определена над k.

Если G - алгебраич. группа над полем 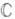, то ее С. к. е. G° совпадает со С. к. е. группы G, рассматриваемой как комплексная группа Ли. Если G определена над 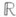, то группа 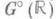вещественных точек в G° не обязательно связна в топологии группы 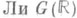, но число ее связных компонент конечно и имеет вид 2^l, где . Напр., группа распадается на две компоненты, хотя 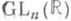связна. Псевдоортогональная унимодулярная группа SO (р, q), к-рая может рассматриваться как группа вещественных точек связной комплексной алгебраич. группы 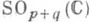, связна при р=0 или q=0 и распадается на две компоненты при р, q> 0.

Лит.:[1] Б о р е л ь А.. Линейные алгебраические группы, пер. с англ., М., 1972; [2]П о н т р я г и н Л. С., Непрерывные группы, 3 изд., М., 1973; [3] Х е л г а с о н С., Дифференциальная геометрия и симметрические пространства, пер. с англ., М., 1964; [4] Ш а ф а р е в и ч И. Р., Основы алгебраической геометрии, М., 1972. А. Л. Онищик.