Akademik

- двупараметрическое семейство линий на плоскости или поверхностей в пространстве, линейно зависящее от параметров. Пусть F₁, F₂, F₃- функции двух переменных, из к-рых ни одна не является линейной комбинацией двух других. Семейство линий на плоскости, определяемых уравнением

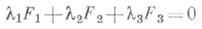
при всевозможных значениях параметров l₁ l₂, l₃ (кроме l₁=0, l₂=0, l₃=0), представляет собой С. (фактически зависит от двух отношений l₁:l₂ : l₃). Аналогично записывается уравнение С. поверхностей в

пространстве. Три уравнения F₁=0, F₂=0, F₃=0дают три элемента С. (три линии или три поверхности), к-рые определяют всю С.

С в я з к а п р я м ы х - множество всех прямых, каждая пара из к-рых лежит в одной плоскости. В евклидовой геометрии С. прямых - множество всех прямых, проходящих через одну точку. Если эта точка конечная, то С. прямых наз. э л л и п т и ч е с к о й, если бесконечно удаленная, - п а р а б о л и ч е с к о й.

С в я з к а п л о с к о с т е й - множество всех плоскостей, проходящих через одну точку (собственная С.) или параллельных нек-рой прямой (несобственная С.).

С в я з к а о к р у ж н о с т е й - двупараметрич. семейство окружностей, линейно зависящее от параметров. Собственной С. окружностей является множество тех окружностей, относительно к-рых данная точка (ц е н т р С.) имеет данную степень точки. Несобственной С. окружностей наз. множество всех окружностей, центры к-рых принадлежат нек-рой фиксированной прямой (т. н. фундаментальной прямой) (см. рис. 1). Если (0,0) - центр собственной связки, то е уравнение

где аи Ь - параметры, определяющие окружность,

р - степень центра С. относительно окружностей С. (степень несобственной С. считается бесконечной). Имеются три типа собственных С. окружностей:

1) г и п е р б о л и ч е с к а я С. (р> 0), состоящая из всех окружностей, ортогональных нек-рой данной окружности (фундаментальной окружности) (см. рис. 2);

2) п а р а б о л и ч е с к а я С. ( р=0), состоящая из всех окружностей, проходящих через нек-рую данную точку (ц е н т р С.) (см. рис. 3);

3) э л л и п т и ч е с к а я С. ( р < 0), состоящая из окружностей, пересекающих нек-рую данную окружность в двух диаметрально противоположных точках последней (см. рис. 4).

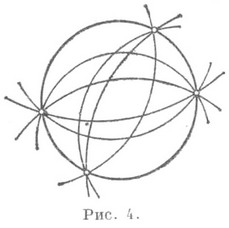
Пересечение двух С. окружностей является пучком окружностей. Эллиптическая С. содержит только эллиптич. пучки, параболическая С.- только эллиптич. и параболич. пучки, гиперболическая С.- три типа собственных пучков. Несобственная С. содержит как несобственные пучки, так и собственные пучки всех трех типов.

Пересечение двух С., из к-рых одна эллиптическая, может быть только эллиптич. пучком. Пересечения двух С., из к-рых одна параболич., может быть только эллиптическим или параболич. пучком. Пересечение двух С., из к-рых одна собственная, может быть только собственным пучком.

С в я з к а с ф е р - двупараметрич. семейство сфер, линейно зависящее от параметров. С. сфер состоит из множества сфер, относительно к-рых точки нек-рой прямой (р а д и к а л ь н о й о с и) имеют одинаковую степень (различную для разных точек). Радикальная ось пересекает все сферы С. в двух точках. В зависимости от того, являются ли эти точки действительными (различными), комплексно сопряженными или совпадающими, С. сфер наз. э л л и п т и ч е с к о й С., к-рая состоит из всех сфер, проходящих через две общие точки; г и п е р б о л и ч е с к о й С., к-рая состоит из всех сфер, ортогональных двум нек-рым пересекающимся сферам; п а р а б о л и ч е с к о й С., к-рая состоит из всех сфер, касающихся нек-рой данной прямой в данной точке. Центры всех сфер С. лежат в одной плоскости, перпендикулярной к радикальной оси.

С. является пересечением всех общих сфер двух сетей сфер.

В проективной геометрии С.- множество всех прямых и плоскостей, проходящих через данную точку.

Лит.:[1] П о с т н и к о в М. М., Аналитическая геометрия, М., 1973; [2] М о д е н о в П. С., Аналитическая геометрия, М., 1969. А. Б. Иванов.