Akademik

- бесконечное произведение вида для всех .

С помощью таких произведений (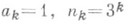 при всех ) Ф. Рисс (F. Riesz) указал первый пример непрерывной функции с ограниченным изменением, коэффициенты Фурье к-рой не равны 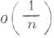. Если q>3,то тождество

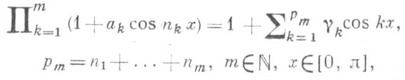
определяет ряд

(2)

о к-ром говорят, что он представляет Р. п. (1). В случае, когда для всех , ряд (2) есть ряд Фурье - Стилтьеса неубывающей непрерывной функции F. Если q>3,

при всех , то F'(x)=0 почти всюду. Если дополнительно 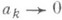, то ряд (2) сходится к нулю почти всюду. Ряд проблем, относящихся в основном к теории тригонометрич. рядов, удалось решить, используя естественное обобщение Р. п., когда в (1) вместо записаны специально выбранные тригонометрич. полиномы .

Лит.:[1] Б а р и Н. К., Тригонометрические ряды, М., 1961; [2] З и г м у н д А., Тригонометрические ряды, пер. с англ., т. 1-2, М., 1965. В. Ф. Емельянов.