Akademik

- зависимость среднего значения какой-либо случайной величины от нек-рой другой величины или от нескольких величин. Если, например, при каждом значении х=x_i наблюдается n_i значений случайной величины Y, то зависимость средних арифметических

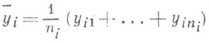
этих значений от x_i и является Р. в статистич. понимании этого термина. При обнаруженной закономерности изменения 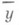с изменением хпредполагается, что в основе наблюдаемого явления лежит вероятностная зависимость: при каждом фиксированном значении хслучайная величина Y имеет определенное распределение вероятностей с математич. ожиданием, к-рое является функцией х:

Зависимость , где хиграет роль "независимой" переменной, наз. р е г р е с с и е й (или ф у н к ц ие й р е г р е с с и и) в вероятностном понимании этого термина. График функции т(х)наз. л и н и е й р ег р е с с и и, или к р и в о й р е г р е с с и и, величины Y по х. Переменная хназ. р е г р е с с и о н н о й п е р е м е н н о й, или р е г р е с с о р о м. Точность, с к-рой линия регрессии Yпо хпередает изменение Yв среднем при изменении х, измеряется дисперсией величины Y, вычисляемой для каждого значения х:

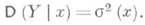
Графически зависимость дисперсии s² (х)от хвыражается т. н. с к е д а с т и ч е с к о й л и н и е й. Если s² (х)=0при всех значениях x, то с вероятностью 1 величины связаны строгой функциональной зависимостью. Если s² (х)№0ни при каком значении хи т (х)не зависит от х, то регрессия Yпо хотсутствует..

В теории вероятностей задача Р. решается применительно к такой ситуации, когда значения регрессионной переменной х соответствуют значениям нек-рой случайной величины Xи предполагается известным совместное распределение вероятностей величин Xи Y(при этом математич. ожидание 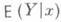и дисперсия 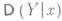будут соответственно условным математич. ожиданием и условной дисперсией случайной величины Yпри фиксированном значении X=x). В этом случае определены две Р.: Y по х и X по у, и понятие Р. может быть использовано также для того, чтобы ввести нек-рые меры взаимосвязанности случайных величин X и Y, определяемые как характеристики степени концентрации распределения около линий Р. (см. Корреляция).

Функции Р. обладают тем свойством, что среди всех действительных функций f(x)минимум математич. ожидания 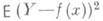достигается для функции f(x)= т (х), то есть регрессия Y по хдает наилучшее (в указанном смысле) представление величины Y. Наиболее важным является тот случай, когда регрессия Y по хл и н е й н а, т. е.

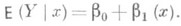
Коэффициенты b₀ и b₁, наз. коэффициентами Р., легко вычисляются:

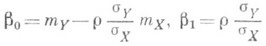
(здесь r - корреляции коэффициент X и Y, ,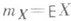

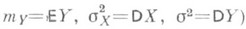, и п р я м а я регрессии Y по х имеет вид

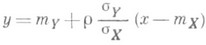
(аналогичным образом находится прямая регрессии Xпо у). Точная линейная Р. имеет место в случае, когда двумерное распределение величин Xи Y является нормальным.

В условиях статистич. приложений, когда для точного определения Р. нет достаточных сведений о форме совместного распределения вероятностей, возникает задача приближенного нахождения Р. Решению этой задачи может служить выбор из всех функций g(x), принадлежащих заданному классу, такой функции, к-рая дает наилучшее представление величины Y в том смысле, что минимизирует математич. ожидание . Найденная функция наз. с р е д н е й к в а д р а т и ч е с к о й Р.

Простейшим будет случай л и н е й н о й с р е д н е й к в а д р а т и ч е с к о й Р., когда отыскивают наилучшую линейную аппроксимацию величины Y посредством величины X, т. е. такую линейную функцию

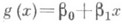, для к-рой выражение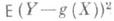

принимает наименьшее возможное значение. Данная экстремальная задача имеет единственное решение

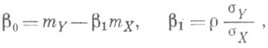
т. е. вычисление приближенной линии Р. приводит к тому же результату, к-рый получен в случае точной линейной Р.:

Минимальное значение 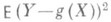при вычисленных значениях параметров равно 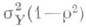. Если регрессия т(х)существует, то при любых b₀ и b₁ имеет место соотношение

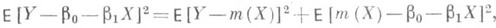
откуда следует, что прямая средней квадратич. регрессии 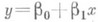дает наилучшее приближение к линии регрессии т(х), если измерять расстояние вдоль оси у. Поэтому если линия т(х)есть прямая, то она совпадает с прямой средней квадратической Р.

В общем случае, когда Р. сильно отличается от линейной, можно поставить задачу нахождения многочлена 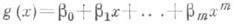нек-рой степени т, для к-рого среднее значение 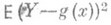имеет возможно меньшее значение.

Такое решение задачи соответствует п а р а б о л ич е с к о й (или п о л и н о м и а л ь н о й) средней квадратической Р. (см. Параболическая регрессия).порядка т. Кривая 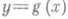есть парабола m-го порядка, дающая наилучшую аппроксимацию истинной линии Р. Обобщением параболической Р. служит функция Р., выраженная линейной комбинацией тех или иных заданных функций:

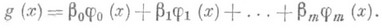
Наиболее важное значение имеет случай, когда j₀ (х), . . .,j_m (х) - ортогональные многочлены соответствующих порядков, построенные по распределению X. Другими примерами н е л и н е й н о й (к р и в о л ин е й н о й) Р. являются случаи тригонометрической Р., показательной Р., и т. п.

Понятие Р. естественным образом обобщается на тот случай, когда вместо одной регрессионной переменной рассматривается нек-рое множество переменных. Если случайные величины X₁ Х₂, . . ., Х _п имеют совместное распределение вероятностей, то множественная Р. определяется, напр., как регрессия X₁ по x₂, . . . , х _п:

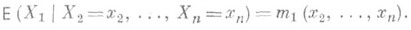
Соответствующее уравнение определяет поверхность регрессии Х ₁ по х₂, . . ., х _n. Линейная регрессия Х ₁ по х ₂, . . ., х _п имеет вид

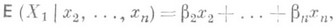
где b₂, . . ., b_n- коэффициенты Р. (при 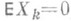). Линейная средняя квадратическая Р. величины Х ₁ по x₂, . . ., х _п определяется как наилучшая линейная оценка величины Х ₁ величинами Х ₂, . .., Х _п в смысле обращения в минимум выражения

Соответствующая п л о с к о с т ь Р. дает наилучшую аппроксимацию поверхности регрессии x₁=m(x₂, . . ., х _п), если последняя существует. Если поверхность Р. есть плоскость, то она необходимо совпадает с плоскостью средней квадратической Р. (так будет в случае, когда совместное распределение всех пвеличин нормально).

Простым примером регрессии Yпо Xявляется зависимость между Yи X, к-рая выражается соотношением 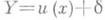, где 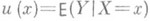, а случайные величины Xи dнезависимы. Это представление полезно, когда планируется эксперимент для изучения функциональной связи у=и (х)между неслучайными величинами уи х. Эта же модель Р. используется во многих приложениях при изучении характера зависимости случайной величины Yот неслучайной величины х. На практике выбор функции у=и (х)и оценку неизвестных коэффициентов Р. по экспериментальным данным производят методами регрессионного анализа.

Лит.:[1] К р а м е р Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975; [2] К е н д а л л М. Д ж., С т ь ю а р т А., Статистические выводы и связи, пер. с англ., М., 1973. А. В. Прохоров.