последовательность точек топологич. пространства, не имеющая предела. Из всякой расходящейся последовательности метрич. компакта можно выделить сходящуюся подпоследовательность. В классе Р. п. нормированных пространств выделяют бесконечно большие последовательности, т. е. такие последовательности { х п}. точек этих пространств, что 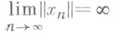
Понятие Р. п. обобщается на кратные последовательности и на направленные (частично упорядоченные) множества. Л. Д. Кудрявцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.