Akademik

системы обыкновенных дифференциальных уравнений

(*)

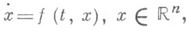- точка такая, что х=xявляется (постоянным по времени) решением системы (*); Р. п. наз. также и само это решение. Точка есть Р. п. системы (*) тогда и только тогда, когда

f(t,x) = 0 при всех t.

Пусть x=j(t) - произвольное решение системы (*). Замена переменных x=j(t)+y переводит это решение в Р. п. y=0 системы

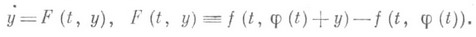
Поэтому, напр., в теории устойчивости без ограничения общности можно считать, что речь всегда идет об исследовании устойчивости Р. п. в начале координат .

Р. п. x=0 неавтономной системы (*) часто наз. тривиальным, или нулевым, решением, а термин Р. п. предпочитают использовать в теории автономных систем обыкновенных дифференциальных уравнений и в теории динамич. систем. Здесь употребляется много синонимов этого термина: особая точка, неподвижная точка, стационарная точка, точка покоя, состояние равновесия.

Н. Х. Розов.