Akademik

распределение вероятностей случайной величины X, принимающей целые неотрицательные значения k=0,1,2, . . ., с вероятностями

где l>0 - параметр. Производящая функция и харак-теристич. функция П. р. определяются соответственно равенствами

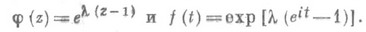
Математич. ожидание, дисперсия и все семиинварианты более высокого порядка равны К. Функция распределения П. р.

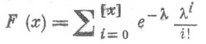
в точках k=0,1,2, . . . выражается формулой

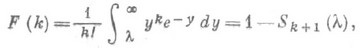
где S_k+1(l) - значение в точке Кфункции гамма-распределения с параметром k+1 (или формулой F(k)=1-H_2k+2(2l), где Н _2k+2(2l) - значение в точке 2lфункции " хи-квадрат" распределения с 2k+2 степенями свободы), откуда, в частности, следует соотношение

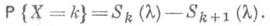
Сумма независимых случайных величин X₁,. . ., X_n имеющих П. р. с параметрами l_l ,. . ., l_n подчиняется П. р. с параметром l₁+...+l _п.

Обратно, если сумма Х ₁+Х ₂ двух независимых случайных величин X₁ и Х ₂ имеет П. р., то каждая случайная величина Х ₁ и Х ₂ подчинена П. р. Имеются общие необходимые и достаточные условия сходимости распределения сумм независимых случайных величин к

П. р. При 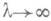случайная величина 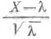имеет в пределе стандартное нормальное распределение.

П. р. было впервые получено С. Пуассоном (S. Роisson, 1837) при выводе приближенной формулы для биномиального распределения в условиях, когда и (число испытаний) велико, а р(вероятность успеха) мало. См. Пуассона теорема2). П. р. с хорошим приближением описывает многие физич. явления (см. [2], т. I, гл. 6). П. р. является предельным для многих дискретных распределений, таких как, напр., гипергеометрическое распределение, отрицательное биномиальное распределение, Пойа распределение, для распределений, возникающих в задачах о размещении частиц по ячейкам при определенном изменении их параметров. В вероятностных моделях П. р. играет большую роль как точное распределение вероятностей. Природа П. р. как точного распределения вероятностей наиболее полно раскрывается в теории случайных процессов (см. Пуассоновский процесс), где П. р. появляется как распределение числа X(t).нек-рых случайных событий, происходящих в течение фиксированного интервала времени t:

(параметр l, - среднее число событий в единицу времени), или, более общо, как распределение случайного числа точек в нек-рой фиксированной области евклидова пространства (параметр распределения пропорционален объему области).

Наряду с П. р., как оно определено выше, рассматривают и так наз. обобщенное или сложное П. р. Так называют распределение вероятностей, суммы X_l+X₂+...+X_v случайного числа v одинаково распределенных случайных величин Х ₁, Х ₂, . . . (при этом v, X₁, Х ₂, . . . считают взаимно независимыми, и v - распределенным по П. р. с параметром l). Характериcтич. функция j(t) обобщенного П. р. равна

где y(t) - характеристич. функция X_v. Напр., отрицательное биномиальное распределение с параметрами n и рявляется обобщенным П. р., так как для него можно положить

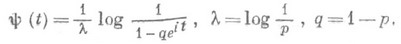
Обобщенные П. р. безгранично делимы и каждое безгранично делимое распределение является пределом обобщенных П. р. (может быть "сдвинутых", т. е. с характеристич. функциями вида .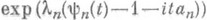

Вместе с тем все безгранично делимые распределения (и только они) могут быть получены как пределы распределений сумм вида 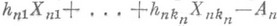, где (X_n1, . . ., X_nkn).образуют схему серий независимых случайных величин с П. р., 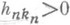и А _п- действительные числа.

Лит.:[1] Poisson S. D., Recherches sur la probabilite des jugements en matlere crlmlnelle et en matiere civile, prfcedees des regies generates du calcul des probabilites, P., 1837; [2] Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., т. 1-2, М., 1967; [3] Большев Л. Н., Смирнов Н. В., Таблицы математической статистики, 2 изд., М., 1968; [4] Линник Ю. В., Островский И. В., Разложения случайных величин и векторов, М., 1972.

А. В. Прохоров.