Akademik

- метрика r( х, у).в подмножестве Rпроективного пространства Р ⁿ такая, что кратчайшая относительно этой метрики является частью или всей проективной прямой. При этом полагают, что Rне принадлежит ни одной гиперплоскости и что 1) для любых трех неколлинеарных точек х, у, z неравенство треугольника выполняется в строгом смысле

r(x, y) +r(y, z) > r(x, z);

2) если х, у - различные точки из R, то пересечение l( х, у).прямой l, проходящей через хи у, с R есть либо вся l(большой круг), либо получается из lудалением нек-poro отрезка (могущего сводиться и к одной точке) (метрическая прямая).

Множества R, наделенные П. м., наз. проективно метрическими пространствами (п. м. п.).

В одном и том же п. м. ц. не могут одновременно существовать оба типа линий: либо все они - метрич. прямые (т. е. изометричны отрезку из 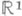), либо же все они - большие круги одинаковой длины (теорема Гамеля). Пространства первого типа наз. открытыми (они совпадают с подмножествами аффинного пространства, то есть с Р ⁿ, из к-рого удалена некрая гиперплоскость); геометрия открытых п. м. п. наз. также Гильберта геометрией. Пространства второго типа наз. замкнутыми (они совпадают со всем Р ⁿ).

Проблема определения всех П. м.- это так наз. 4-я проблема Гильберта (см. [2]), полное ее решение дано А. В. Погореловым (1974).

С П. м. связано, как частный ее случай, т. н. проективное мероопределение- введение в подмножества проективного пространства методами проективной геометрии такой метрики, при к-рой эти подмножества оказываются изоморфными евклидову, гиперболическому и эллиптическому пространствам. Так, геометрия открытых п. м. п., подлежащее множество к-рых совпадает со всем аффинным пространством, наз. геометрией Минковского. Евклидова геометрия - это одновременно геометрия Гильберта и геометрия Минковского.

Гиперболическая геометрия - геометрия Гильберта, в к-рой существуют отражения от всех прямых. Для этого необходимо и достаточно, чтобы R было внутренностью эллипсоида.

Эллиптическая геометрия (или Римана геометрия) - геометрия п. м. п. второго типа.

Лит.:[1] Буземан Г., Келли П. Д да.. Проективная геометрия и проективные метрики, пер. с англ., М., 1957; 12J Проблемы Гильберта, пep. с нем., М., 1969.

М. И. Войцеховский.