множество точек 3-мерного действительного (или комплексноро) пространства, координаты к-рых в декартовой системе удовлетворяют алгебраич. уравнению 2-й степени
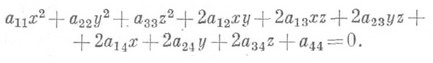 (*)
(*)
Уравнение (*) может и не определять действительного геометрич. образа, в таких случаях говорят, что уравнение (*) определяет мнимую П. в. п. В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного переноса и поворота системы координат на нек-рый угол к одному из 17 приведенных ниже канонич. видов, каждому из к-рых соответствует определенный класс поверхностей. Именно, невырождающиеся нераспадающиеся поверхности:
 - эллипсоид,
- эллипсоид,
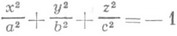 -мнимый эллипсоид,
-мнимый эллипсоид,
 - однополостный гиперболоид,
- однополостный гиперболоид,
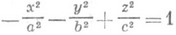 -двуполостный гиперболоид,
-двуполостный гиперболоид,
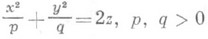 - эллиптический параболоид,
- эллиптический параболоид,
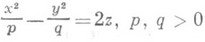 - гиперболический параболоид;
- гиперболический параболоид;
вырождающиеся нераспадающиеся поверхности:
цилиндрические поверхности, -
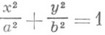 - эллиптический цилиндр,
- эллиптический цилиндр,
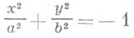 -мнимый эллиптический цилиндр,
-мнимый эллиптический цилиндр,
 - гиперболический цилиндр, у 2 = 2рх -параболический цилиндр';
- гиперболический цилиндр, у 2 = 2рх -параболический цилиндр';
конические поверхности -
 - коническая поверхность,
- коническая поверхность,
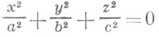 -мнимая коническая поверхность;
-мнимая коническая поверхность;
вырождающиеся распадающиеся поверхности:
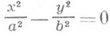 - пара пересекающихся плоскостей,
- пара пересекающихся плоскостей,
 - пара мнимых пересекающихся плоскостей,
- пара мнимых пересекающихся плоскостей,
 - пара параллельных плоскостей,
- пара параллельных плоскостей,
х 2 + а 2=0 -пара мнимых параллельных плоскостей.
x2= 0 -пара совпадающих плоскостей.
П. в. п., имеющие единственный центр симметрии (центр П. в. п.), наз. центральными поверхностями. Координаты центра определяются решением системы:

П. в. п. без центра симметрии или с неопределенным центром наз. нецентральными поверхностями.
Исследование П. в. п. может быть осуществлено без приведения общего уравнения к канонич. виду. Это достигается совместным рассмотрением значений т. н. основных инвариантов П. в. п.- выражений, составленных из коэффициентов уравнения (*), значения к-рых не меняются при параллельном переносе и повороте системы координат:

и семиинвариантов (полуинвариантов) D' и D", к-рые являются инвариантами относительно поворота системы координат: D' = D11 + D22 + D33, где Dij - алгебраич. дополнение элемента а ik, в D;

См. табл. 1 и 2.
Табл. 1. - Классификация поверхностей второго порядка по инвариантам
| | Невырождающиеся поверхности | Вырождающиеся поверхности | ||||
| D > 0 | D < 0 | D = 0 | ||||
| Центральные поверхности d не равно 0 | dS> 0, Т> 0 | Мнимый эллипсоид | Эллипсоид | Мнимый конус | ||
| | Однополост-ный гиперболоид | Двуполост-ный гиперболоид | Действительный конус | |||
| Центральные поверхности d=0 | | Гиперболический параболоид | Эллиптический параболоид | Цилиндрические и распадающиеся поверхности (см. табл. 2) | ||
Табл. 2. -Цилиндрические и распадающиеся поверхности второго порядка (D= 0, d = 0)
| | Цилиндрические поверхности | Распадающиеся поверхности | ||||
| Т>0 | Эллиптический цилиндр | Пара мнимых пересекающихся плоскостей | | |||
| Мнимый D'S> 0 | Действительный D'S< 0 | |||||
| Т<0 | Гиперболический цилиндр | Пара пересекающихся плоскостей | ||||
| Т= 0 | Параболический цилиндр | Пара мнимых параллельных плоскостей D"> 0 | Пара совпадающих плоскостей D"=0 | |||
| Пара параллельных плоскостей D"< 0 | ||||||
Инварианты в общем случае определяют П. в. п. с точностью до движения евклидова пространства, если соответствующие инварианты двух поверхностей равны, то такие поверхности могут быть совмещены движением. Иными словами, эти поверхности эквивалентны по отношению к группе движений пространства (метрически эквивалентны).
Существует классификация П. в. п. с точки зрения других групп преобразований. Так, относительно группы аффинных преобразований эквивалентными являются любые две поверхности, определяемые уравнениями одного канонич. вида, напр. две подобные П. в. н. являются эквивалентными.
Связи между различными аффинными классами П. в. п. позволяет установить классификация с точки зрения проективной геометрии. При этом эквивалентными считаются поверхности, к-рые могут быть переведены друг в друга посредством проективного преобразования. Напр., эллипсоиды, эллиптич. параболоиды и двуполостные гиперболоиды с точки зрения проективной геометрии являются действительными овальными поверхностями. Их проективная эквивалентность проявляется в том, что существует нек-рая система проективных координат, в к-рой уравнения этих поверхностей имеют одинаковый вид:

т. е. соответствующие квадратичные формы Ф ( х 1, х 2, х 3, x4) имеют одинаковые ранг (4) и сигнатуру (3). Аффинное их различие проявляется в типе линии пересечения с несобственной плоскостью: эллипсоиды пересекаются с ней по мнимому овалу, гиперболоиды - по действительному овалу, эллиптич. параболоиды - по паре мнимых пересекающихся прямых. Всего существует 8 классов проективной эквивалентности П. в. п.:
 -мнимая овальная поверхность,
-мнимая овальная поверхность,
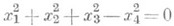 - действительная овальная поверхность,
- действительная овальная поверхность,
 -кольцевидная поверхность,
-кольцевидная поверхность,
 - мнимая коническая поверхность,
- мнимая коническая поверхность,
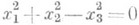 - действительная коническая поверхность,
- действительная коническая поверхность,
 - пара мнимых плоскостей,
- пара мнимых плоскостей,
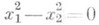 - пара действительных плоскостей,
- пара действительных плоскостей,
 - пара совпадающих плоскостей.
- пара совпадающих плоскостей.
Лит. см. при ст. Линия второго порядка. А. Б. Иванов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.