Akademik

координаты прямой в трехмерном пространстве, шесть чисел р ₀₁, p₀₂, p₀₃, p₀₄, p₀₅, p₀₆ из к-рых первые три являются координатами направляющего вектора lпрямой L, а вторые три - моменты этого вектора относительно начала координат. Пусть прямая Lпроходит через точки X и Y с проективными координатами ( х ₀, x₁, . .., x₃).и (y₀, y₁, . . ., y₃).соответственно П. к. этой прямой являются числа

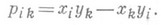
П. к. применяют в линейчатой геометрии. Впервые были рассмотрены Ю. Плюккером (J. Plucker, 1869). Иногда вместо П. к. используют Клейна координаты ( х ₀, . . ., х ₅), связанные с П. к. формулами:

Естественно рассматривать П. к. как координаты в р-мерном векторном подпространстве n-мерного векторного пространства V. При этом они понимаются как совокупность чисел, равных 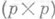- субдетерминантам -матрицы ( а ₁, а ₂, . . ., а _р), столбцы а _i, , к-рой являются столбцами координат (в каком-либо базисе пространства V).базисных векторов подпространства W. Если - компоненты столбца то П. к. (или грассмановы координаты) являются числа

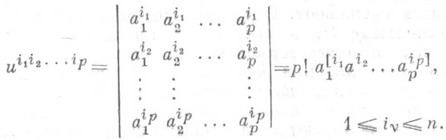
П. к. симметричны по всем индексам. Число существенных П. к. равно .

При замене базиса Wи фиксированном базисе VП. к. умножаются на одно и то же ненулевое число. При замене базиса Vи фиксированном базисе WП. к. преобразуются как координаты контравариантного тензора валентности р (см. Поливектор). Два подпространства совпадают тогда и только тогда, когда их П. к., вычисленные в одном и том же базисе пространства V, отличаются лишь ненулевым множителем.

Принадлежность вектора хподпространству Wзаписывается в виде линейных уравнений

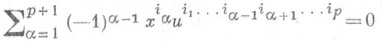
с коэффициентами, являющимися П. к. подпространства W. В этих уравнениях i₁<i₂<. . .<i_p- всевозможные наборы из чисел 1, 2, . . ., п. Л. П. Купцов.