Akademik

- задача нахождения минимальной поверхности (м. п.) с заранее заданной границей Г. Впервые такая задача была поставлена Ж. Лагранжем (J. Lagrange, 1760), к-рый свел ее в классе поверхностей вида z=z( х, у).к решению уравнения Эйлера - Лагранжа м. п. После опытов Ж. Плато (J. Plateau, 1849), в к-рых он показал, что м. п. могут быть получены в виде мыльных пленок, натянутых на проволочные каркасы (см. [1]), эту задачу стали называть задачей Плато.

В строгой постановке П. з. требует ряд дополнительных уточнений, относящихся к искомой м. п. и к ее границе. Напр., должно ли искомое решение быть регулярной м. п. или же его можно искать среди обобщенных минимальных поверхностей (о. м. п.); обязательно ли искомая поверхность должна реализовать абсолютный минимум площади; каков должен быть конформный или топологич. тип поверхности; в каком смысле понимать границу поверхности, и т. п. В зависимости от постановки задачи, ее решения и свойства этих решений (существование, единственность, регулярность и т. д.) могут быть существенно различными.

В течение 19 в. П. з. была решена для нек-рых частных видов заданной границы Г, главным образом для различных полигональных контуров. В 1928 было доказано существование решения П. з. для о. м. п. типа круга, представляемой формулами Вейерштрасса и ограниченной заданной незаузленной жордановой кривой. В 1931 дано решение П. з. в следующей формулировке: пусть Г- жорданова кривая в тогда в существует о. м. п., заданная в изотермич. координатах ( и, v).радиус-вектором r=r(u, v), непрерывным в круге 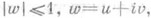и гомеоморфно отображающим окружность |w| = 1 на Г; при этом площадь этой о. м. п. оказывается наименьшей среди всех непрерывных поверхностей типа круга, натянутых на контур Г, в предположении, что на Г можно натянуть хотя бы одну такую поверхность конечной площади.

После решения П. з. в 1931 для односвязной поверхности Дж. Дуглас (J. Douglas) поставил вопрос (т. н. задача Дугласа) о существовании в , , м. п., имеющей заданный топологич. тип (т. е. заданную эйлерову характеристику и характер ориентируемости) и ограниченной заданным контуром Г, состоящим из объединения жордановых кривых . В 1936-40 были даны достаточные условия разрешимости этой задачи, одно из к-рых заключается в возможности натянуть на Г какую-нибудь поверхность данного топологич. типа, площадь к-рой была бы меньше, чем площадь любой поверхности с меньшей эйлеровой характеристикой, натянутой на тот же контур. В такой постановке П. з. была рассмотрена и решена также в римановом пространстве.

В нач. 60-х гг. 20 в. было достигнуто большое продвижение и в решении П. з. для k-мерных поверхностей, . Было предложено несколько обобщений П. з., основанных на новых определениях понятий поверхности, границы и площади. Одно из обобщений исходит из следующего определения понятия поверхности Xи ее границы Lв 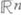. Пусть имеются компакт 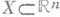и компакт - абелева группа и - целое число; тогда определены группы гомологии Чеха - Александрова и ; ядро гомоморфизма , индуцированного вложением 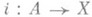, наз. алгебраич. границей компакта X(в размерности k).по отношению к А . Если L - подгруппа группы 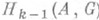, то Xявляется поверхностью с границей , если Lпринадлежит алгебраич. границе компакта X;под площадью компакта Xв понимается его k-мерная хаусдорфова (сферическая) мера . При таких определениях доказаны существование и регулярность почти всюду (топологическая локально евклидовость и аналитичность) компакта Х ₀, реализующего минимум меры 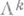по всем компактам Xс заданной границей L. Впоследствии эти теоремы были распространены на случай поверхностей Xв римановом пространстве.

Другие предложенные обобщения П. з., в частности обобщение в терминах интегральных потоков, являются в нек-ром смысле эквивалентными постановке П. з. в терминах гомологии.

В классич. постановке Плато многомерная задача решена в 1969; а именно, доказана теорема: если в римановом пространстве Vⁿ задано (k-1)-мерное подмногообразие 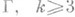, то существует поверхность, реализующая минимум хаусдорфовой меры среди всех параметризуемых поверхностей X, являющихся в Vⁿ непрерывными f-образами k-мерных гладких многообразий М с краем, гомеоморфным Г при отображении .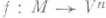

Наряду с вопросами разрешимости П. з. интересными являются также вопросы единственности и регулярности ее решения. Наиболее продвинуто исследование вопроса о регулярности решения. Показано, что решение П. з., данное Дугласом в , не содержит внутренних точек ветвления. Для случая многомерной П. з. доказана регулярность решения почти всюду, причем возможность наличия нерегулярных точек подтверждается примерами. Что касается единственности решения П. з., то здесь известны лишь нек-рые достаточные признаки единственности (напр., решение П. з. единственно, если заданный контур Г имеет однозначную выпуклую проекцию при центральном или параллельном проектировании на нек-рую плоскость). Чтобы подчеркнуть сложность этого вопроса, достаточно сказать, что есть основания ожидать существование спрямляемых контуров, стягивающих континуум м. п. типа круга.

Лит.:[1] Encyklopadie der mathematischen Wissenschaften, Bd 3, H. 2/3, Lpz., 1903; [2] Darboux G., Leconssur la theorie generate des surfaces..., 2 ed., pt. 1, P., 1914; [3] Вianch i L., Vorlesungen iiber Differentialgeometrie, 2 Aufl., Lpz.- В., 1910; [4] Куpaнт Р., Принцип Дирихле, конформные отображения и минимальные поверхности, пер. с англ., М., 1953; [5] Моrrеу С., "Ann. Math.", 1948, v. 49, М 4, p. 807 - 51; [6] Radо Т., On the problem of Plateau, В., 1933; [7] Hиче И. С. С., "Математика", 1967, т. 11, № 3, с. 37-100; [8] Оссерман Р., там же, 1971, т. 15, № 2, с. 104-25; [9] Фоменко А. Т., "Изв. АН СССР. Сер. матем.", 1972, т. 36, с. 1049- 1079; [11] Nitsсhе J. С. С., "Invent, math.". 1969, v. 8, N 4, p. 313-33; [12] Оссерман Р., "Успехи матем. наук", 196V, т. 22, в. 4, с. 55-136; [13] Federer H., Geometric measure theory, В.- [u. a.], 1969; [14] Моrrеу С., Multiple integrals in the calculus of variations, B.- [u. a.], 1966. И. Х. Сабитов.