Akademik

для каждой квадратично суммируемой функции интеграл

сходится в L₂ к нек-рой функции при ,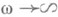

то есть

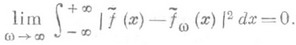
При этом сама функция f(х).представляется как предел в L₂ при интегралов

то есть

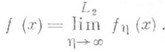
Кроме того, справедливо соотношение

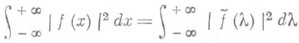
(формула Парсеваля - Планшереля). Функция

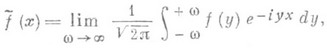
где предел понимается в смысле сходимости в L₂, наз. преобразованием Фурье функции f и обозначается обычным символом

(1)

при этом интеграл (1) понимается в смысле главного значения на 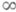в метрике L₂. Аналогично истолковывается равенство

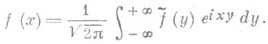(2)

Для функции 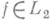интегралы (1) и (2) существуют в смысле главного значения почти при всех х.

Функции f и 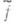удовлетворяют почти при всех хтакже соотношениям

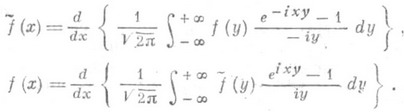
Если обозначить 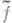преобразование Фурье, 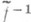- его обращение, то П. т. перефразируется так: 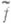и - взаимно обратные унитарные операторы в L₂.

П. т. установлена М. Планшерелем (М. Plancherel, 1910).

Лит.:[1] Зигмунд А,, Тригонометрические ряды, пер. с англ., т. 2, М., 1965; [2] Титчмарш Е., Введение в теорию интегралов Фурье, пер. с англ., М.- Л., 1948; [3] Бохнер С., Лекции об интегралах Фурье, пер. с англ., М., 1902. П. И. Лизоркин.