Akademik

инвариантная форма леммы Шварц а,- обобщение Шварца леммы, состоящее в следующем. Пусть w=f(z) - ограниченная регулярная аналитич. ция в единичном круге

.

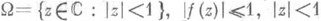Тогда для любых точек z₁ и z₂ круга W. неевклидово расстояние d(w₁, w₂).их образов w₁=f(z₁).и w₂=f(z₂).не превосходит неевклидова расстояния d(z₁, z₂), то есть

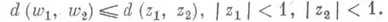(1) Кроме того, имеет место неравенство

(2)

между элементами неевклидовой длины (дифференциальная форма П. т., или леммы Шварца). Знаки равенства в (1) и (2) имеют место только в том случае, когда w=f(z) есть дробно-линейная функция, отображающая круг W на себя.

Неевклидово, или гиперболическое, расстояние d(z₁, z₂) есть расстояние в геометрий Лобачевского между точками z₁ и z₂, когда круг Wпринимается в Качестве плоскости Лобачевского, а прямыми Лобачевского служат дуги окружностей, ортогональных единичной окружности (Модель Пуанкаре); при этом

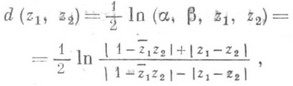
где - двойное отношение точек z₁, z₂ и определяемых этими точками точек пересечения ос, Р прямой Лобачевскому проходящей через z₁ и z₂, с единичной окружностью (см. рис.).

Неевклидова длина образа f(L).любой Спрямляемой кривой 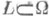при отображении w=f(z) не превосходит неевклидовой длины L.

П. т. была установлена Г. Пиком (см. [1]); дальнейшим ее обобщением является гиперболической метрики принцип. В геометрич. теории функций из этих теорем выводятся оценки различных функционалов, связанных с отображающей функцией (см. [2], [3]).

Лит.:[1] Рiсk G., "Math. Ann.", 1916, Bd 77, S. 1-6; [2] Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [3] Каратеодори К., Конформное отображение, пер. с англ., М.- Л., 1934.

К. Д. Соломенцев.