Akademik

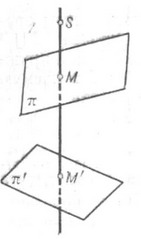
с центром S- отображение плоскости p в плоскость p', при к-ром каждой точке Мплоскости p ставится в соответствие точка М' пересечения прямой SM с плоскостью p' (если прямая SM не параллельна плоскости p'; см. рис.).

В проективной геометрии П. определяется следующим образом: пусть Vи V' - собственные подпространства одинаковой размерности проективного пространства W, Т - подпространство максимальной размерности, не имеющее общих точек ни с V, ни с V'. Пусть U - подпространство, содержащееся в V, и W- подпространство минимальной размерности, содержащее Uи Т, а U' - пересечение Wи V'.

Соответствие, при к-ром каждому подпространству U, содержащемуся в V, ставится в соответствие подпространство U', содержащееся в V', наз. перспективным отображением пространства Vна пространство V' с центром перспективы Т.

П. есть коллинеация. Если подпространства Vи V' пересекаются, то каждая точка подпространства сама себе соответствует.

Если в пространствах Vи V' введены проективные координаты, то перспективное соответствие может быть задано линейным отображением.

Лит.:[1] Артин Э., Геометрическая алгебра, пер. с англ., М., 1969; [2] Глаголев Н. А., Проективная геометрия, 2 изд., М., 1963. П. С. Моденов.