Akademik

- отображение, сопоставляющее точке s базы Sсемейства 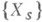алгебраич. многообразий над полем С комплексных чисел когомо-логии 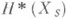слоя над этой точкой, снабженные Ходжа структурой. Полученная при этом структура Ходжа рассматривается как точка в многообразии модулей структур Ходжа данного типа.

Изучение О. п. восходит к исследованиям Н. Абеля (N. Abel) и К. Якоби (С. Jacobi) интегралов алгебраич. функций (см. А белев дифференциал). Однако до недавнего времени глубоко были изучены лишь О. п., отвечающие семействам кривых.

Пусть 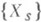есть семейство слоев гладкого проективного морфизма 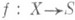, где S - гладкое многообразие. Тогда когомологии снабжены чистой, поляризованной структурой Ходжа, к-рая задается гомоморфизмом вещественных алгебраических групп где С* - мультипликативная группа С* поля комплексных чисел, рассматриваемая как вещественная алгебраич. группа, а

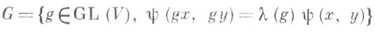
- алгебраич. группа линейных преобразований пространства V, умножающих невырожденную (симметрическую или кососимметрическую) билинейную форму y на скалярный множитель; причем автоморфизм Ad h(i).группы является инволюцией Картана и 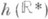лежит в центре группы 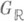. Множество X_G гомоморфизмов 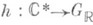, обладающих указанными свойствами, естественным образом снабжено 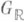-инвариантной структурой однородного кэлерова многообразия и наз. многообразием Гриффитса, а фактор 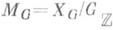является пространством модулей

структур Ходжа. Гомоморфизм h задает разложение Ходжа

алгебры Ли 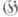группы G, где 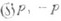- подпространство в на к-ром Ad h(z) действует умножением на 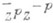. Сопоставление 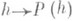, где Р(h).- параболич. подгруппа в 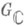, алгебра Ли к-рой есть

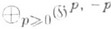, задает открытое плотное вложение многообразия X_G в компактное -однородное многообразие флагов . В касательном пространстве

к X_G в точке hвыделено горизонтальное подпространство

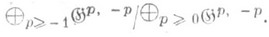
Голоморфное отображение в X_G или M_G наз. горизонтальным, если образ его касательного отображения лежит в горизонтальном подрасслоении.

Установлено, что О. п. горизонтально (см. [1], [3]). Особенности О. п. описываются теоремой Шмида о нильпотентной орбите, к-рая в случае, когда 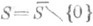- кривая с выколотой точкой, утверждает, что если z- локальная координата на S, z(0) = 0, то при Ф (z) асимптотически близко к

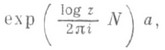
где , а - нильпотентный элемент (см. [4]). Относительно группы монодромии

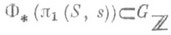
известно, что ее образ полупрост во всяком рациональном представлении группы G, а преобразования обхода Т вокруг дивизора с нормальными пересечениями 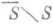в гладкой компактификации 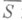многообразия Sпорождают квазпунипотентные (т. е. имеющие в качестве собственных значений корни из 1) элементы 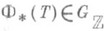. Важность группы монодромии подчеркивает теорема жесткости (см. [1], [2], [4]): если над Sимеются два семейства алгебраич. многообразий, то соответствующие О. и. 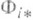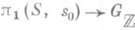Ф ₁ н Ф ₂ из Sв M_G совпадают тогда и только тогда, когда Ф ₁(s₀)=Ф ₂(s₀) в нек-рой точке и гомоморфизмы : , i=l, 2, совпадают.

Законченные результаты о строении ядра и образа О. п. относятся в основном к случаям кривых и КЗ-поверхностей. Если {X_s} - семейство многообразий указанного типа и Ф (s)= Ф (s'), то 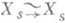, (теорема Торелли), а для КЗ-поверхностей максимально возможный образ О. п. совпадает с M_G (см. [7]). В случае кривых образ О. п. частично описан (соотношения Шоттки - Юнга, см. [6], [8]). Существует гипотеза Гриффитса о том, что многообразие модулей допускает частичную аналитич. омпактификацию, т. е. открытое вложение в такое аналитич. ространство , что О. п. 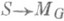продолжается до голоморфного отображения для всякой гладкой компакти-фикации . Такая компактификация известна (1983) лишь для случая, когда X_G- симметрическая область [9].

Лит.:[1] Гриффитс Ф, А., "Успехи матем. наук", 1970, т. 25, в. 3, с. 175-234; [2] Griffiths Ph. А., в кн.: Actes du Congres international des mathematicians (Nice), 1970, t. 1, P., 1971, p. 113-19; [3] De1igne P., Travaux de Griffiths, в кн.: Seminaire Bourbaki. 1969/70, В.- N. Y,- Hdlb., 1971, p. 213-35; [4] Schmid W., "Invent, math.", 1973, v. 22, p. 211-319; 15] Сattani E. Н., Кap1an A. G., "Duke Math. J.", 1977, v. 44, № 1, p. 1-43; [6] Дубровин Б. А., "Успехи матем. наук", 1981, т. 36, в. 2, с.11-80; [7] Куликов В. А., там же, 1977, т. 32, в. 4, с. 257-58; [8] Мамфорд Д., "Математика", 1973, т. 17, № 4, с. 34-42; [9] Вai1у W., Воrеl A., "Ann. Мath", 1966, V. 84, р. 442-528. А. И. Овсеевич.