Akademik

один из методов математич. анализа, позволяющий в ряде случаев сводить исследование дифференциальных операторов, псевдодифференциалъных операторов и нек-рых типов интегральных операторов и решение уравнений, содержащих эти операторы, к рассмотрению более простых алгебраич. задач. Развитие и систематич. применение О. и. началось с работ О. Хевисайда (О. Heaviside, 1892), к-рый предложил формальные правила обращения с оператором дифференцирования и решил ряд прикладных задач. Однако О. и. не получило у него математич. обоснования: оно было дано с помощью Лапласа преобразования;Я. Микусиньский (J. Mikusinski, 1953) алгебраизировал О. и., опираясь на понятие функционального кольца; наиболее общая концепция О. и. получается с помощью обобщенных функций.

Простейший вариант О. и. строится следующим образом. Пусть К - совокупность функций (с действительными или комплексными значениями), заданных в области и абсолютно интегрируемых в любом конечном интервале. Сверткой функций наз. интеграл

Относительно обычного сложения и операции свертки Кстановится кольцом без делителей нуля (теорема Титчмарша, 1924). Элементы поля частных Рэтого кольца наз. операторами и обозначаются ; невыполнимость деления в Ккак раз и есть источник нового понятия оператора, обобщающего понятие функции. Для выявления необходимого в О. и. различия между понятиями функции и ее значения в точке введены следующие обозначения:

{f(t)} - функция f(t).

f(t) - значение t (t).в точке t.

Примеры операторов. 1) е={1} -оператор интегрирования:

при этом

и, в частности,

это - формула Коши, обобщение к-рой на случай произвольного (нецелого) показателя служит для определения дробного интегрирования.

2). (где a - функция-константа) -числовой оператор; поскольку [а] [b] = [a, b], [a] {f}={af}, в то время как {a}{b}={abt}, то числовые операторы ведут себя как обычные числа. Таким образом, оператор является обобщением не только функции, но и числа; единицей кольца Кявляется [ 1 ].

3) - оператор дифференцирования, обратный оператору интегрирования. Так, если функция a(t)--{a(t)}имеет производную a'(t), то

и

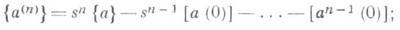
отсюда, напр.,

На оператор дифференцирования s можно умножать не только дифференцируемые функции, однако результат есть уже, вообще говоря, оператор.

4) - алгебраическая производная, она распространяется на произвольные операторы обычным способом, при этом оказывается, что действие этого оператора на функции от sсовпадают с дифференцированием по s.

О. и. дает удобные способы решения линейных дифференциальных уравнений как обыкновенных, так и с частными

производными. Напр., решение уравнения удовлетворяющее начальным условиям х(0).g₀, . . .,

автоматически приводится к алгебраич. уравнению и символически выражается формулой

решение в обычном виде получается разложением на элементарные дроби от переменной s с последующим обратным переходом по соответствующим таблицам к функциям.

Для применения О. и. к уравнениям с частными производными (а также к более общим псевдодифференциальным уравнениям) строятся дифференциальное и интегральное исчисления операторных функций, т. е. функций, значениями к-рых являются операторы: вводятся понятия непрерывности, производной, сходимости ряда, интеграла и т. д.

Пусть f(l, t) - нек-рая функция, определенная для и .Параметрическая операторная функция f(l) определяется формулой f(l)={f(l, t)};она ставит в соответствие рассматриваемым значениям l операторы частного вида - функции от t. Операторная функция наз. непрерывной при , если она представима как произведение нек-рого оператора qи такой параметрич. функции f₁(l)={f₁(l, t)}, что f₁(l, t).непрерывна в обычном смысле.

Примеры. 1) С помощью параметрич. функции h(l)={h(l,t)}:

определяется функция Хевисайда

значения гиперболической показательной функции

наз. операторами сдвига, поскольку умножение данной функции на 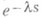вызывает смещение ее графика на длину l в положительном направлении оси t.

2) Решение уравнения теплопроводности

выражается через параболическую показательную функцию (являющуюся также параметрической операторной функцией):

3) Периодич. функция f(t).с периодом 2l₀ имеет представление

4) Если f(l) принимает числовые значения в интервале [l₁, l₂], то

т. е. умножение данной функции {/} на с последующим интегрированием вызывает усечение ее графика. В частности,

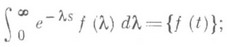
таким образом, каждой функции f(t), для к-рой рассматриваемый интеграл сходится, ставится в соответствие аналитич. ция

- ее преобразование Лапласа. Благодаря этому обстоятельству довольно обширный класс операторов описывается функциями одного параметра s, более того, это формальное сходство уточняется математически установлением определенного изоморфизма.

Имеются различные обобщения О. и.; таково О. и. дифференциальных операторов, отличных от , напр. , к-рое основывается на функциональных кольцах с надлежащим образом определенным произведением.

Лит.:[1] Д и т к и н В. А., Прудников А. П., Справочник по операционному исчислению, М., 1965; [2] Микусинский Я., Операторное исчисление, пер. с польск., М., 1956.

М. И. Войцеховский.

А-ОПЕРАЦИЯ, операция А, - теоретико-множественная операция, открытая П. С. Александровым [1] (см. также [2] с. 39 и [3]). Пусть - система множеств, заиндексированных всеми конечными последовательностями натуральных чисел. Множество

где суммирование распространяется на все бесконечные последовательности натуральных чисел, наз. результатом A-O., примененной к системе

Применение A-O. к системе интервалов числовой прямой дает множества (названные А-множествами в честь П. С. Александрова), к-рые могут не быть борелевскими (см. Дескриптивная теория множеств). A-O. сильнее операции счетного объединения и счетного пересечения и является идемпотентной. Относительно А-О. инвариантны Бэра свойство (подмножеств произвольного топологич. пространства) и измеримость по Лебегу.

Лит.:[1] Александров П. С., "С. г. Acad. sci", 1916, t. 1P>2, p. 323-25; [2] его ж е, Теория функций действительного переменного и теория топологических пространств, М., 1978; [3] Колмогоров А. Н., "Успехи матем. наук", I960, т. 21, в. 4, с. 275-78; [4] Суслин М. Я., "С. г. Acad. sci.", 1917, t. 164, p. 88-91; 15] Лузин Н. Н., Собр. соч., т. 2, М., 1958, с. 284; [6] Куратовский К., Топология, пер. [с англ.], т. 1, М., 1966. А. Г. Ельцин.

ds-ОПЕРАЦИЯ - теоретико-множественная операция, результат применения к-рой к последовательности (E_n) множеств может быть записан в виде

где N - система множеств положительных целых чисел, наз. базой ds=0. См. Дескриптивная теория множеств.

Лит.:[1] К о л м о г о р о в А. Н., "Матем. сб.", 1928, т. 35, №3-4, с. 415-22; [2] X а у с д о р ф Ф., Теория множеств, пер. с нем., М.- Д., 1937; [3] Александров П. С., Теория функций действительного переменного и теория топологических пространств, М., 1978, с. 35-40, 53-58; [4] О ч а н Ю. С., "Успехи матем. наук", 1955, т. 10, в. 3, с. 71 - 128; [5] Колмогоров А. Н., там же, 1966, т. 21, в. 4, с. 275-78. А. Г. Елькип.