Akademik

- замкнутая выпуклая -гладкая линия в . Точки О., в к-рых кривизна достигает экстремума, наз. вершинами О. Число вершин О. не менее четырех.

Пусть Е- О ., пробегаемый против часовой стрелки, в плоскости с декартовыми прямоугольными координатами х, y; h- расстояние ориентированной касательной к Еот начала О (h> 0, если вращение касательной вокруг Опроисходит против часовой стрелки). Тогда уравнение касательной

где - угол касательной с осью Ох. Величина 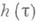наз. опорной функцией О. Радиус кривизны

длина О. (формула Коши):

Между длиной Lи площадью Fобласти внутри О. выполняется соотношение

(уточнение см. в ст. Боннезена неравенство).

А. Б. Иванов.