Akademik

- частично рекурсивная функция, определенная для всех значений аргументов. Понятие О. ф. может быть определено и независимо от понятия частично рекурсивной функции следующим образом. Класс всех О. ф.- это наименьший класс функций, содержащий все примитивно рекурсивные функции и замкнутый относительно композиции функций и наименьшего числа оператора при условии, что последний применяется к функции лишь тогда, когда

Однако изучение О. ф. обычно ведется в классе всех частично рекурсивных функций. Это связано, в частности, с тем, что ни при каком натуральном n>0 не существует О. ф., универсальной для класса всех n-местных О. ф.

Все О. ф. нумерически представимы в арифметике формальной, так что для любой такой функции можно построить арифметич. формулу обладающую следующим свойством: каковы бы ни были натуральные числа 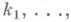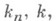если 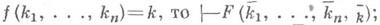если же , - термы, изображающие числа k₁ , . .., k _п , k, символ означает выводимость в арифметич. исчислении.

Лит.:[1] Новиков П. С, Элементы математической логики, 2 изд., М., 1973; [2] Мендельсон Э., Введение в математическую логику, пер. с англ., М., 1971.

В. Е. Плиспо.