нормированное уравнение, прямой на плоскости - уравнение вида
где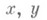 
- декартовы прямоугольные координаты плоскости; 
и 
- координаты единичного вектора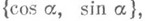 
перпендикулярного к прямой; 
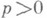- расстояние от начала координат до прямой. К Н. у. уравнение прямой вида
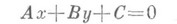
приводится умножением на нормирующий множитель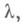 
модуль к-рого есть 
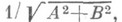а знак противоположен знаку С(при С=0 знак 
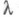можно выбирать произвольно).
Аналогично случаю прямой, уравнение плоскости
приводится к Н. у.
где 
- направляющие косинусы вектора, перпендикулярного к плоскости, умножением на нормирующий множитель 
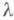, модуль к-рого есть 
а знак 
противоположен знаку D.
А. Б. Иванов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.