Akademik

- методы вычисления пределов функций, заданных формулами, к-рые в результате формальной подстановки в них предельных значений аргумента теряют смысл, т. е. переходят в выражения типа

по к-рым нельзя судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют. Основным инструментом для раскрытия неопределенностей служит Тейлора формула, с помощью к-рой выделяется главная часть функции. Так, в случае неопределенности типа 0/0, для того чтобы найти предел

где

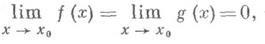
функции fи g представляют по формуле Тейлора в окрестности точки х ₀ (если это возможно) до первого не равного нулю члена:

в результате получается, что

В случае неопределенности типа для нахождения предела

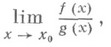
где

применяют преобразование

сводящее задачу к раскрытию неопределенности типа 0/0.

Неопределенности типа и также целесообразно приводить к виду 0/0 следующими преобразованиями:

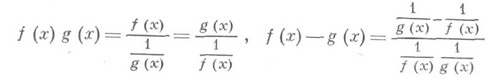
соответственно.

Для раскрытия неопределенностей типа 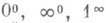целесообразно первоначально прологарифмировать выражения, предел к-рых требуется найти.

Другим общим методом раскрытия неопределенностей типа . и .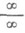. и сводимых к ним является Лопита ля правило.

Л. Д. Кудрявцев.