Akademik

теории функций комплексного переменного - первоначально (Н. з. по Адамару) задачи для дифференциальных уравнений с характером неустойчивости, аналогичным неустойчивости задачи Коши для уравнения Лапласа. Для задач этого типа строится пример Ада мара - вариации данных, сколь угодно малые вместе с любым конечным числом своих производных, к-рым соответствуют конечные вариации решений (см. [2] , [5]). Ныне термин "Н. з." понимается значительно шире (см. [1], [6]).

Задачи аналитич. родолжения теории функций комплексного переменного (одного) являются Н. з. по Адамару. Такую задачу для функций одного комплексного переменного в общем виде можно сформулировать следующим образом. Задана область Dкомплексной плоскости и заданы два множества А, В, принадлежащие замыканию . На множестве Азадана аналитич. ция f(z), регулярная в области D. Требуется определить функцию f(z) на множестве В. Относительно функции f(z), кроме регулярности в D, может быть задана дополнительная информация, напр.

где С- заданная константа.

Классич. задачами аналитич. родолжения являются следующие: 1) А- подобласть области D;2) А- часть границы Г области D;предполагается, что Г - непрерывно (кусочно) дифференцируемая замкнутая кривая, 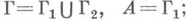3) А- множество, имеющее предельную точку внутри D.

Теоремы единственности отмеченных задач были доказаны в 19 в. (они приводятся в учебниках по теории функций комплексного переменного). Задача 2 эквивалентна задаче Коши для уравнения Лапласа.

Оценки условной устойчивости задач аналитич. родолжения типа 1), 2) наз. теоремами о трех константах (оценка изменения решения задачи через изменение данных при условии типа (*)). Задачи аналитич. родолжения являются линейными, и к ним применимы универсальные методы регуляризации линейных Н. з. (см. [3], [6]). Для задачи 2). разработаны специальные методы регуляризации, основанные на построении функций Карлемана (см. [3]).

Задачи аналитич. родолжения связаны с широким кругом прикладных проблем. Часто из физич. законов следует, что различные физич. поля являются аналитич. циями по нек-рым переменным. Требуется по значениям поля на нек-ром множестве (на к-ром производятся измерения) определить поле на более широком множестве. Нек-рые из этих прикладных задач следующие.

1. Задача определения гравитационного и магнитного поля над поверхностью Земли по значениям поля на поверхности. Эта задача используется при разведке месторождений полезных ископаемых.

2. Задача определения потенциала течения идеальной жидкости, фильтрации постоянного электрич. тока внутри нек-рого тела по значениям потенциала и потока на части поверхности (см. [4]).

3. Задача определения финитной функции по значениям преобразования Фурье этой функции, известным на конечном отрезке.

С точки зрения приложений значит, интерес представляет задача определения аналитич. ции по ее значениям на конечных множествах. Решение этой задачи не единственно. Однако если множество в нек-ром смысле близко к множеству единственности, возможно приближенное решение с малой погрешностью.

Для функций нескольких комплексных переменных существуют как корректные, так и некорректные задачи аналитич. родолжения. Для задач аналитич. родолжения с множеств внутри области регулярности известен следующий общий результат: для того чтобы множество было множеством единственности, необходимо и достаточно, чтобы это множество не являлось объединением конечного числа аналитич. многообразий.

Лит.:[1] Иванов В. К., Васин В. В., Танана В. П., Теория линейных некорректных задач и ее приложения, М., 1978; [2] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964; [3] Лаврентьев М. М., О некоторых некорректных задачах математической физики, Но-восиб., 1962; [4] Лаврентьев М. А., Шабат Б. В., Методы теории функций комплексного переменного, 2 изд., М., 1958; [5] Соболев С. Л., Уравнения математической физики, 4изд., М., 1966; [6] Тихонов А. Н., Арсенин В. Я., Методы решения некорректных задач, М., 1974; [7] Фукс Б. А., Теория аналитических функций многих комплексных переменных, 2 изд., ч. 1, М., 1962.

М. М. Лаврентьев.