Akademik

-Частный случай метода спуска, когда направление , указывающее спуск, выбирается противоположным 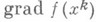Формулы Н. с. м. имеют вид

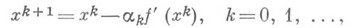
где параметры выбираются из условия максимального убывания на каждом шаге функции . Если функция дважды непрерывно дифференцируема и матрица 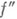ее вторых производных удовлетворяет при любых х, у неравенству

с констадтами 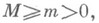то (см. [2], [4]) последовательность 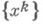сходится к решению задачи минимизации функции f со скоростью геометрич. прогрессии со знаменателем q<1.

Широкое применение Н. с. м. нашел при решении систем линейных алгебраич. уравнений Ax=f с эрмитовой и положительно определенной матрицей А. В действительном случае задача решения этой системы эквивалентна нахождению вектора 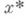, минимизирующего в пространстве n-мерных векторов функционал

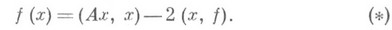
Применительно к (*) формулы Н. с. м. принимают вид

причем значение определяется из условия минимума функционала (*) по формуле

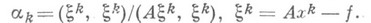
Если спектр матрицы Апринадлежит отрезку действительной оси 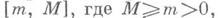то последовательность 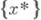сходится к решению 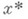со скоростью геометрич. прогрессии со знаменателем

Н. с. м. может быть применен для решения операторного уравнения 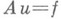с самосопряженным положительно определенным ограниченным оператором А. Если оператор Ане удовлетворяет наложенным условиям, задачу можно симметрировать, сведя к задаче

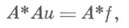
и уже затем применить Н. с. м. (см. также Минимальных невязок метод).

Лит.:[1] Канторович Л. В., "Докл. АН СССР", 1947, т. 56, № 3, с. 233-36; [2] Канторович Л. В., Акилов Г. П., Функциональный анализ, 2 изд., М., 1977; [3] Фаддеев Д. К., Фаддеева В. Н., Вычислительные методы линейной алгебры, 2 изд., М.- Л., 1963; [4] Пшеничный Б. Н., Данилин Ю. М., Численные методы в экстремальных задачах, М., 1975; [5] Бахвалов Н. С, Численные методы, 2 изд., т. 1, М., 1975.

Ю. А. Кузнецов.