Akademik

- наименьшее положительное из общих кратных целых, в частности натуральных, чисел . Н. о. к. чисел существует, если . Н. о. к. чисел обычно обозначают символом

Свойства Н: о. к.:

1) Н. о. к. чисел - делитель любого общего кратного этих чисел;

2)

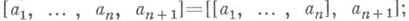
3) если целые числа представлены в виде

где - различные простые,

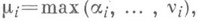и то

4) если где - наибольший общий делитель для аи b.

Последнее свойство позволяет находить Н. о. к. двух чисел при помощи Евклида алгоритма. Понятие Н. о. к. может быть введено для элементов области целостности, а также для идеалов коммутативного кольца.

Лит.:[1] Виноградов И. М., Основы теории чисел, 9 изд., М., 1981; [2] Бухштаб А. А., Теория чисел, 2 изд., М., 1966; [3] Фор Р., Кофман А., Дени-Папен М., Современная математика, пер. с франц., М., 1966.

В. И. Нечаев, А. А. Бухштаб.