Akademik

- линейный метод приближения, обеспечивающий на заданном множестве 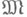приближаемых элементов наименьшую, по сравнению с другими линейными методами, погрешность. В линейном нормированном пространстве Xлинейный метод приближения элементов элементами фиксированного подпространства задается линейным оператором, отображающим все пространство Xили нек-рое, содержащее , линейное многообразие в F. Если 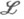- совокупность всех таких операторов, то Н. л. м. для множества (если он существует) определяется оператором 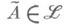, для к-рого

Метод, определяемый оператором Аиз 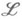, заведомо является Н. л. м. для 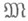относительно приближающего множества F, если для всех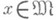

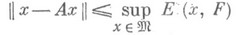
(Е( х, F)- наилучшее приближение элемента хмножеством F)и, тем более, если для всех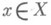

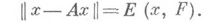
Последний факт имеет место, когда X - гильбертово пространство,есть n-мерное (n=1, 2, ...) его подпространство, А- линейный оператор ортогонального проектирования на 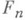, т. е.

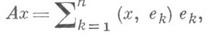
где - ортонормированный базис в F_n.

Пусть X - банахово пространство заданных на всей действительной оси функций с нормой, инвариантной относительно сдвига: (этому условию удовлетворяет, напр., норма пространств 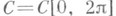и 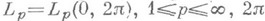-периодических функций), 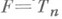- подпространство тригонометрич. полиномов порядка п. Для класса функций из X, содержащего вместе с x(t)также и z(t+a) при любом существуют Н. л. м. (относительно Т _n), в частности Н. л. м. вида

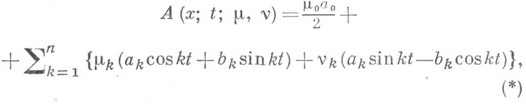
где 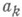и - коэффициенты Фурье функции x(t)по тригонометрич. системе, 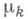и 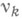- нек-рые числа.

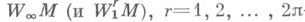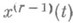На классах -периодических функций , у к-рых производная локально абсолютно непрерывна, а 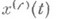по норме в (соответственно в 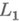) ограничена числом М, Н. л. м.

вида (*) дает в метрике пространства С(соответственно L₁ )ту же погрешность (на всем классе), что и наилучшее приближение подпространством 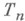; аналогичный факт имеет место для таких классов при любом дробном (производная понимается в смысле Вейля). При целых r=1, 2, ... Н. л. м. вида (*) строится только с помощью коэффициентов 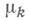(все ).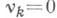

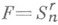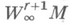
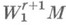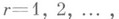Если - подпространство 2p-периодических полиномиальных сплайнов порядка rдефекта 1 по разбиению то для классов (и ), Н. л. м. в 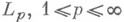(соответственно в L₁), доставляют сплайны из 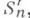, интерполирующие функцию в точках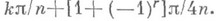

Лит.:[1] Ахиезер Н. И., Лекции по теории аппроксимации, 2 изд., М., 1965; [2] Корнейчук Н. П., Экстремальные задачи теории приближения, М., 1976; [31 Тихомиров В. М-, Некоторые вопросы теории приближений, М., 1976- Н. П. Корнейчук, В. П. Моторный