Akademik

- наилучшее приближение функции кпеременных алгебраическими или тригонометрич. многочленами. Пусть X- пространство Сили 2p-периодических по каждому переменному функций 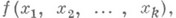непрерывных либо суммируемых со степенью на k-мерном кубе периодов.

Н. п. п. функции тригонометрич. полиномами есть величина

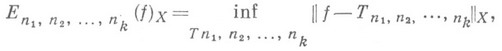
где точная нижняя грань берется по всевозможным тригонометрич. полиномам порядка 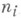от переменных . Наряду с Н. п. п. функции f рассматриваются частные наилучшие приближения этой функции.

Наилучшее частное приближение функции - есть наилучшее приближение функциями 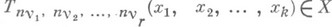, являющимися тригонометрич. полиномами степени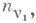 соответственно от фиксированных переменных 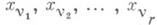с коэффициентами, зависящими от остальных k- r переменных, т. е. величина

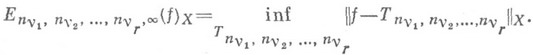
Очевидно, что

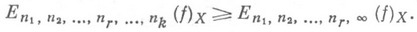
Для непрерывных функций двух переменных С. Н. Бернштейн [1] доказал неравенство

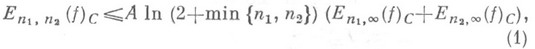
где А- абсолютная константа. Установлено [31, что в неравенстве (1) (и в аналогичном соотношении для пространства L₁) нельзя заменить 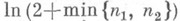на множитель, растущий при min 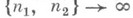медленнее. В пространстве 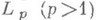имеет место неравенство

где постоянная A_p,k зависит только от ри k.

Аналогично определяются Н. п. п. и наилучшее частное приближение функций, заданных в замкнутой ограниченной области 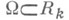алгебраическими многочленами, и в этом случае известны неравенства вида (1), (2).

Лит.:[1] Бернштейн С. Н., Собр. соч., т. 2, М., 1954; [2] Тиман А. Ф., Теория приближения функций действительного переменного, М., 1960; [3] Темляков В. Н., "Докл. АН СССР", 1975, т. 223, № 5, с. 1079-82.

Н. П. Корнейчук, В. П. Моторный.