Akademik

наилучшего приближения полином,- многочлен, осуществляющий наилучшее приближение функции в той или иной метрике среди всех многочленов, построенных по той же (конечной) системе функций. Если X - линейное нормированное пространство функций (напр., или ) ,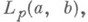

- система линейно независимых функций из X, то для любой 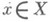(обобщенный) Н. п. м.

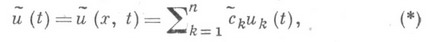
определяемый соотношением

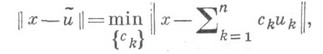
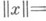
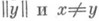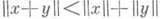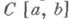существует. Единственность Н. п. м. для всех имеет место, во всяком случае, если X- пространство со строго выпуклой нормой (т. е. из следует, что ). Таким является пространство при . В пространстве , норма к-рого не является строго выпуклой, Н. п. м. для любой единствен, если система 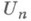является чебышевской на т. е. каждый многочлен

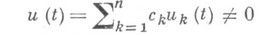
имеет на отрезке 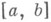не более чем нулей. В частности, единственность имеет место для алгебраич. многочленов в а также для тригонометрич. полиномов в пространстве непрерывных на всей оси периодических функций с равномерной метрикой. Если Н. п. м. существует и единствен для любой то он непрерывно зависит от х.

Известны критерии, указывающие необходимые и достаточные признаки Н. п. м. в пространствах 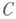и 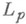Справедлива, напр., теорема Чебышева: если система 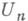является чебышевской, то для того, чтобы многочлен (*) являлся для функции 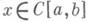Н. п. м. в метрике пространства 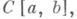необходимо и достаточно, чтобы нашлась система из 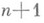точек 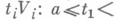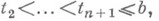в к-рых разность

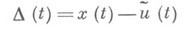
принимает значения

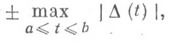
причем

Многочлен (*) является Н. п. м. для функции 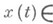в метрике этого пространства тогда и только тогда, когда

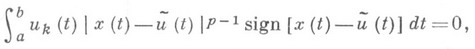
k=1, 2, ... , п. В случае р=1, т. е. в пространстве L₁[a, b], условия

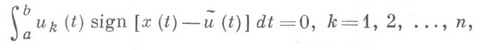
достаточны, а если мера множества тех точек tиз ( а, b), где 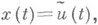равна нулю, то и необходимы, чтобы был Н. п. м. для 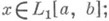см. также Маркова крите рий.

Существуют алгоритмы приближенного построения многочленов наилучшего равномерного приближения (см., напр., [3], [5]).

Лит.:[1] Ахиезер Н. И., Лекции по теории аппроксимации, 2 изд., М., 1965; [2] Корнейчук Н. П., Экстремальные задачи теории приближения, М., 1976; [3] Дзядык В. К., Введение в теорию равномерного приближения функций полиномами, М., 1977; [4] Тихомиров В. М., Некоторые вопросы теории приближений, М., 1976; [5] Лоран П. Ж., Аппроксимация и оптимизация, пер. с франц., М., 1975; [6] Ремез Е. Я., Основы численных методов чебышевского приближения, К., 1969.

H. П. Корнейчук, В. П. Моторный.