Akademik

первого и второго рода - собственные значения монодромии оператора канонич. уравнений.

В комплексном гильбертовом пространстве уравнения вида где - самосопряженные операторы,периодичен, наз. каноническими. В конечномерном случае собственные числа оператора монодромии для этого уравнения наз. мультипликаторами. Если все решения канонич. уравнения являются ограниченными на всей оси (уравнение устойчиво), то М. лежат на единичной окружности. Если рассмотреть канонич. уравнение 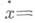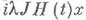с действительным параметром, то все М.

делятся на две группы: М. 1-го (2-го) рода, к-рые движутся против (по) часовой стрелке при увеличении параметра

Канонич. уравнение наз. сильно устойчивым, если оно устойчиво и остается устойчивым при достаточно малых вариациях оператора . Для сильной устойчивости необходимо и достаточно, чтобы все М. лежали на единичной окружности и чтобы не было совпадающих М. разного рода.

Теория М. 1-го и 2-го родов позволила получить ряд тонких признаков устойчивости и оценок зон устойчивости для канонич. уравнений. В терминах М. проведена гомотопич. классификация устойчивых и неустойчивых канонич. уравнений.

Лит.:[1] Далецкий Ю. Л., Крейл М. Г., Устойчивость решений дифференциальных уравнений в банаховом пространстве, М., 1970; [2] Якубович В. А., Старжинский В. М., Линейные дифференциальные уравнения с периодическим! коэффициентами и их приложения, М., 1972.

С. Г. Kрейн.