Akademik

- понятие, естественным образом обобщающее понятие однолистной функции. Функция 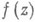, регулярная или мероморфная в области Dкомплексной плоскости z, наз. р-листной в D(р=1, 2, ...), если она принимает в этой области каждое свое значение не более рраз, т. е. если число корней уравнения 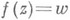в области Dпри любом w не превосходит р. Геометрически это означает, что над каждой точкой плоскости wлежит не более рточек римановой поверхности, на к-рую функция отображает область D. При р=1 функция f(z) является однолистной в области D.

Наряду с этим простейшим классом р-листных функций большую роль в теории М. ф. играют функции, р-листные в нек-ром обобщенном смысле, "р-листные в среднем". Пусть функция 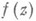регулярна или мероморфна в области Dплоскости z,- число корней уравнения 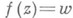в Dи р - положительное число.

Функция наз. р-листной в среднем по окружности в D, если для всех 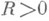выполняется условие:

Геометрически это означает, что линейная мера дуг, принадлежащих римановой поверхности, на к-рую функция отображает область D, и проектирующихся в любую окружность 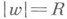, не превосходит р длин таких окружностей. Функция f(z) наз. р-листной в среднем по площади в D, если

для всех . Геометрически это означает, что площадь проектирующейся в любой круг 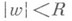части римановой поверхности, на к-рую функция отображает область D, не превосходит р площадей таких кругов. Из этих определений следует, что функция, р-листная в нек-рой области, является в ней и р-листной в среднем по окружности, а функция, р-листная в среднем по окружности, является р-листной в среднем по площади. Функция, р-листная в среднем, может оказаться бесконечнолистной.

М. ф., как и однолистные, изучаются в различных направлениях: с точки зрения характеристики искажения области при ее отображениях этими функциями, оценки коэффициентов рядов, представляющих эти функции, и т. д. Они обладают многими экстремальными свойствами, аналогичными экстремальным свойствам однолистных функций. Напр., имеются следующие обобщения на случай р-листных функций двух классич. результатов теории однолистных функций - площадей принципа и оценки второго коэффициента (см. Вибербаха гипотеза). Если функция

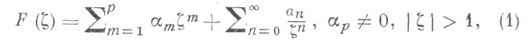
р-листна и регулярна в области , за исключением полюса в точке 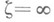, то

Если функция

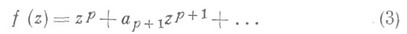
регулярна и р-листна в круге |z|<1, то

Неравенства (2) и (4) не могут быть улучшены. Эти два результата относятся к наиболее ранним основным результатам теории р-листных функций. Неравенство (2) доказано также для функций вида (1), р-листных в среднем по площади в , а неравенство (4) - для функций вида (3), р-листных в среднем по площади в

Значительно продвинуть исследование класса р-листных функций позволило рассмотрение его как подкласса функций, р-листных в среднем. Получены для р-листных функций и точные аналоги основных теорем искажения и покрытия, известных для однолистных функций (см. Искажения теоремы, Покрытия теоремы), именно: для функций f(z) вида (3), р-листных в среднем по окружности в круге |z|<1, верны точные оценки:

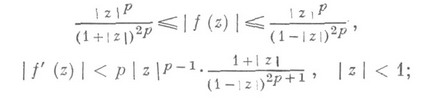
функция f(z)принимает в |z|<l каждое значение wс 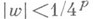ровно р раз (прямой аналог теоремы покрытия Кебе). Этим последним свойством обладают и функции 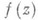вида (3), р-листные в среднем по площади в 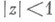. Для функций, р-листных в среднем по окружности, получен ряд неулучшаемых результатов, характеризующих рост их коэффициентов. Так, для функции вида

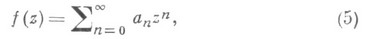
р-листной в среднем по окружности в круге 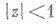, , 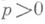существует, и притом конечный, предел

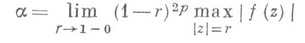
и

при 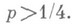Всякий раз, когда получается оценка для , отсюда следует и соответствующая точная оценка асимптотич. роста коэффициентов. В частности, если 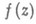имеет вид (3), то последнее равенство принимает вид

где 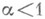, за исключением того случая, когда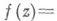 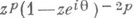(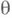- вещественно). Далее, для функций вида (3), р-листных в среднем по окружности в круге , получена точная оценка:

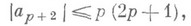
а для подкласса р-листных функций такого вида была указана точная оценка и следующего коэффициента:

Два последних неравенства являются для М. ф. аналогами оценок и , известных для однолистных функции (см. Бибербаха гипотеза). Так. как экстремальными функциями приведенных выше оценок оказываются р-листные функции, то все эти результаты не могут быть улучшены и в классе р-листных функций. Для функций вида (5), р-листных в среднем по площади в круге 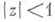, известны следующие оценки их коэффициентов для всех :

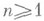и оценка

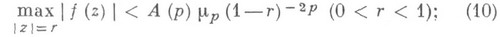
здесь 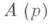зависит только от Порядок величин в (6), (9) и (10) не может быть улучшен.

Имеется также следующий аналог для М. ф. теоремы, известной для однолистных мероморфных функций: в классе всех функций

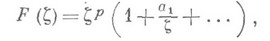
р-листных и регулярных в области за исключением полюса в имеющих в фиксированной точке этой области разложение

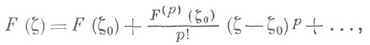
областью значений функционала

является круг

Кроме указанных выше основных классов М. ф., значительное место в исследованиях занимают, более специальные классы М. ф., напр, функции типично вещественные порядка р, р-листно звездные, р-листно выпуклые, р-листно близкие к выпуклым, ограниченные р-листные и др., являющиеся обобщениями соответственно типично вещественных функций, звездообразных функций, выпуклых функций, близких к выпуклым, ограниченных однолистных и других функций.

Функция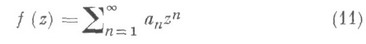

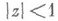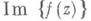наз. типично вещественной порядка р в круге , если она регулярна в нем, имеет вещественные коэффициенты и обладает свойством: существует такое число что для всякого г из промежутка мнимая часть меняет свой знак на окружности точно 2р раз.

При этом 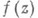может быть более чем р-листной в Для коэффициентов такой функции имеет место точная оценка:

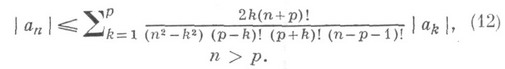
Одним из аналогов гипотезы Бибербаха для функций вида (11), регулярных и р-листных в круге , является гипотеза Гудмена о справедливости для их коэффициентов неравенства (12). В частности, эта гипотеза Гудмена верна для р-листных типично вещественных функций порядка р в Доказано, что она верна также для одного из классов р-листных функций, являющегося обобщением класса однолистных функций, выпуклых в направлении мнимой оси. Другим аналогом гипотезы Бибербаха для р-листных функций является следующая гипотеза Гудмена. Пусть функция

регулярна и р-листна, 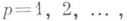в круге 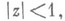и пусть она имеет tнулей в области 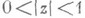, 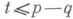. Гипотеза состоит в том, что 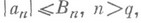где - коэффициенты разложения

Для типично вещественных функций порядка р в 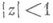это неравенство доказано.

Классы р-л истно звездных и р-листно выпуклых функций, соответственно 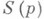и 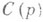, определяются следующим образом. Функция принадлежит классу если она регулярна в круге 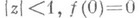и если существует такое число , что

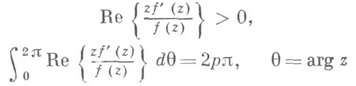
для 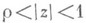. Функция f(z)принадлежит классу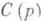 , если она регулярна в круге 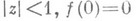и если существует такое 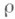, что

для 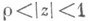. Для функций этих двух классов получен ряд точных оценок.

Классы и 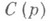оказываются подклассами более широкого класса р -листных функций - функций р-листно близких к выпуклым. Функция

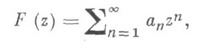
регулярная в круге , наз. р-листно близкой к выпуклой, если она удовлетворяет одному из следующих условий:

(А) существуют функция 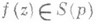и число 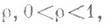такие, что

(Б) F(z)регулярна на |z|=l и существует функция , также регулярная на |z| = l, такая, что на |z| = l выполняется неравенство (13). Для функций F(z)этого класса найдены точные оценки снизу и сверху |F'(z)|и доказана справедливость неравенства (12) - при n=p+l для всех функций этого класса и при всех для его функций с вещественными коэффициентами. Точные оценки, обобщающие нек-рые результаты для ограниченных однолистных функций, получены и для ограниченных функций, р-листных в соответствующем обобщенном смысле. Так, был найден радиус р-листности в классе регулярных и ограниченных в круге функций, именно: если функция f(z)регулярна и ограничена по модулю единицей в круге |z|<l, нормирована условиями 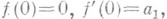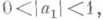то радиус р наибольшего круга , в к-ром она р-листна, определяется из уравнения

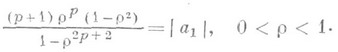
Эта теорема обобщает на случай р>1 теорему Ландау о радиусе однолистности функций, регулярных и ограниченных в круге .

Известны различные достаточные условия для того, чтобы функция, регулярная в области, была в ней р-листной. Напр., если регулярна в выпуклой области D и существуют такое вещественное и такое целое что

то f(z) р -листна в D,

М. ф. исследуются также и в многосвязных областях. Многие оценки здесь выражаются через функции, отображающие данную мвогосвязную область на канонические римановы поверхности, и через Бергмана керн-функцию. Первым основным результатом, относящимся к вопросу существования конформных отображений многосвязной области на многолистные канонич. поверхности, явилась следующая теорема Грунского: пусть D- конечносвязная область плоскости z с внутренней точкой и с отличными от точек граничными компонентами и 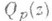- любой заданный полином степени 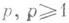; тогда для любого заданного 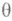, 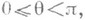существует единственная функция 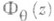, регулярная в области D, за исключением полюса в 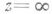, главная часть к-рой в (с включением в нее свободного члена) совпадает с 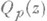н к-рая ставит в соответствие каждой граничной компоненте области Dпрямолинейный отрезок наклона 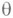к вещественной оси. Иначе говоря, функция отображает область Dна полную р-листную плоскость wс параллельными разрезами наклона 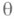. Доказано существование конформных отображений данной конечносвязной области и на другие канонические многолистные поверкности; установлены экстремальные свойства М. ф., аналогичные нек-рым экстремальным свойствам однолистных функций. Выявлен просто характеризуемый геометрически наиболее общий класс М. ф., мероморфных в конечно-связной области, для к-рых верна теорема площадей.

Основными методами исследования М. ф. являются: контурного интегрирования метод, симметризации метод, метод квадратичных дифференциалов.

Вариационный метод в теории М. ф. менее эффективен, чем в теории однолистных функций.

Лит.:[1] Голузин Г. М., "Матем. сб.", 1940, т. 8, в. 2, с. 277-83; [2] Xейман В. К., Многолистные функции, пер.

с англ., М., 1960; [3] Дженкинс Дж., Однолистные функции и конформные отображения, пер. с англ., М., 1962; [4] Pethe К., "Bull. Acad. Polon. Sci.", 1372, v. 20, № 3, p. 219-20; [5] Livingston A. E., "Trans. Amer. Math. Soc", 1965, v. 115, № 3, p. 161-79; [6] Leасh R. J., "Pacific J. Math.", 1978, v. 74, №1, p. 133-42; [7] Кrzуz J., "Ann. Univ. Mariae Curie-Sklodowska. Sec. A", 1958, v. 12, № 2, p. 23-28, № 3, p. 29-38; [8] Оzaki S., "Sci. Rep. Tokio Bunrika Daigaku", A, 1935, v. 2, № 40, p. 167-88; [9] Аленидын Ю. Е., "Изв. АН СССР. Сер. матем.", 1973, т. 37, № 5, с. 1132-54; [10] S inch S. К., "Math. Student", 1962, v. 30, №. 1-2, p. 79-90: [11] Goodman A. W., "Bull. Amer. Math. Soc", 1968, v. 74, №. 6, p. 1035-50.

Ю. Е. Аленицын.