Akademik

асимптотический ряд по последовательности

или по последовательности

(см. Асимптотическое разложение функции). А. с. р. можно складывать, перемножать, делить и интегрировать точно так же, как и сходящиеся степенные ряды. Пусть функции и имеют при асимптотич. разложения:

Тогда

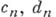( вычисляются по тем же правилам, что и для сходящихся степенных рядов);

4) если функция 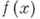непрерывна при , то

5) А. с. р. не всегда можно дифференцировать, однако, если имеет непрерывную производную, к-рая разлагается в А. с. р., то

Примеры А. с. р.:

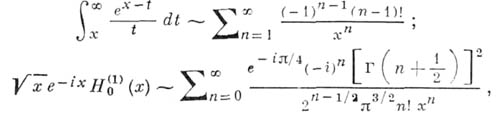
где 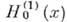- Ганкеля функция нулевого порядка (приведенные А. с. р. расходятся при всех х).

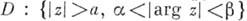Аналогичные утверждения имеют место и для функций комплексного переменного при в окрестности бесконечно удаленной точки или внутри угла. В случае комплексного переменного утверждение 5) имеет следующий вид: если функция регулярна в области и если

равномерно по 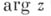при 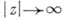в любом замкнутом угле, содержащемся в D, то

равномерно по 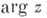при в любом замкнутом угле, содержащемся в D.

Лит.:(1) Копсон Э. Т., Асимптотические разложения, пер. с англ., М., 1966; (2) Эрдейи А., Асимптотические разложения, пер. с англ., М., 1962; (3) Уиттекер Э. Т., Ватсон Дж. П., Курс современного анализа, пер. с англ., 2 изд., т. 1, М., 1962. М. И. Шабунин.