- одна из числовых характеристик распределения вероятностей, частный случай квантили. Для действительной случайной величины Xс функцией распределения F(х)М. наз. число то, к-рое удовлетворяет условиям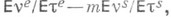 
и 
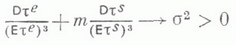. Любая случайная величина имеет по крайней мере одну М. Если F(x) = 1/2 при всех хиз замкнутого интервала, то каждая точка этого интервала есть М. Если F(х)строго монотонная функция, то М. единственна. В симметричном случае М., если она единственна, совпадает с математич. ожиданием, если последнее существует. Тот факт, что М. существует всегда, используется для центрирования случайных величин (см., напр., Леей неравенство). В математич. статистике для оценки М. распределения по независимым результатам наблюдений Х 1, ..., Х п используют т. н. выборочную медиану - М. соответствующего вариационного ряда Х (1), . . ., Х (п):величину Х (k+ 1),если п=2к+1 -нечетное, и 
если п-2к - четное.
Лит.:[1] Лоэв М., Теория вероятностей, пер. с англ., М., 1962; [2] Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975.
А. В. Прохоров.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.