Akademik

теоретическая логика, символическая логика,- раздел математики, посвященный изучению математич. доказательств и вопросов оснований математики.

Исторический очерк. Идея построения универсального языка для всей математики и формализации на базе такого языка математич. доказательств выдвигалась в 17 в. Г. Лейбницем (G. Leibniz). Но только в сер. 19 в. появились первые научные работы по алгебраизации аристотелевод логики [Дж. Буль (G. Boole, 1847) и О. де Морган (A. de Morgan, 1858)]. После того как Г. Фреге (G. Frege, 1879) и Ч. Пирс (С. Peirce, 1885) ввели в язык алгебры логики предикаты, предметные переменные и кванторы, возникла реальная возможность применить этот язык к вопросам оснований математики.

С другой стороны, создание в 19 в. неевклидовой геометрии сильно поколебало уверенность математиков в абсолютной надежности геометрич. интуиции, на к-рой была основана евклидова геометрия. Сомнениям в надежности геометрич. интуиции способствовало также то, что в результате развития исчисления бесконечно малых математики натолкнулись на неожиданные примеры всюду непрерывных функций без производных. Появилась потребность отделить понятие действительного числа от неясного понятия "величины", к-рое было основано на геометрич. интуиции. Эта задача была решена разными путями в работах К. Вейерштрасса (К. Weierstrab, P. Дедекинда (R. Dedekind) и Г. Кантора (G. Cantor). Они показали возможность "арифметизации" анализа и теории функций, в результате чего в качестве фундамента всей классич. математики стала рассматриваться арифметика целых чисел. Затем была предпринята аксиоматизация арифметики [Р. Дедекинд (1888) и Дж. Пеано (G. Реаnо, 1891)]. При этом Дж. Пеано создал более удобную символику для логич. языка. Пвзже этот язык был усовершенствован в совместном труде Б. Рассела (В. Russell) и А. Уайтхеда (A. Whitehead) "Принципы математики" (1910), где была предпринята попытка сведения всей математики к логике. Но эта попытка не увенчалась успехом, т. к. оказалось невозможным вывести из чисто логич. аксиом существование бесконечных множеств. Хотя логистич. программа Фреге - Рассела в основаниях математики так и не достигла своей главной цели - сведения математики к логике, в их работах был создан богатый логич. аппарат, без к-рого оформление М. л. как полноценной математич. дисциплины было бы невозможно.

На рубеже 19-20 вв. были обнаружены антиномии, связанные с основными понятиями теории множеств. Наиболее сильное впечатление на современников произвела опубликованная в 1903 антиномия Рассела. Пусть Месть множество всех таких множеств, каждое из к-рых не является своим собственным элементом. Легко убедиться, что Мявляется своим элементом тогда и только тогда, когда Мне является своим элементом. Конечно, можно пытаться выйти из создавшегося противоречия, сделав заключение, что такого множества Мне бывает. Однако, если не может существовать множество, состоящее в точности из всех элементов, удовлетворяющих такому четко определенному условию, к-рое мы имеем в приведенном выше определении множества М, то где гарантия того, что в нашей повседневной работе мы не столкнемся с множествами, к-рые также не могут существовать? И каким, вообще, условиям должно удовлетворять определение множества для того, чтобы оно существовало? Ясно было одно: нужно как-то ограничить канторовскую теорию множеств .

Л. Брауэр (L. Brouwer, 1908) выступил против применения правил классич. логики к бесконечным множествам. В выдвинутой им интуиционистской программе предлагалось отказаться от рассмотрения абстракции актуальной бесконечности, т. е. бесконечных множеств как завершенных совокупностей! Допуская существование сколь угодно больших натуральных чисел, интуиционисты выступают против рассмотрения натурального ряда как завершенного множества. Они считают, что в математике всякое доказательство существования того или иного объекта должно быть конструктивным, т. е. должно сопровождаться построением этого объекта. Если предположение о том, что искомый объект не существует, приведено к противоречию, то это, по мнению интуиционистов, не может рассматриваться как доказательство существования. Особой критике со стороны интупционистов подвергся исключенного третьего закон. Ввиду того, что этот закон первоначально рассматривался применительно к конечным множествам и, учитывая, что многие свойства конечных множеств не выполняются для бесконечных множеств (напр., что всякая собственная часть меньше целого), интуиционисты считают неправомерным применение этого закона к бесконечным множествам. Так, напр., чтобы утверждать, что проблема Ферма имеет положительное решение или имеет отрицательное решение, интуиционист должен указать соответствующее решение этой проблемы. А пока проблема Ферма не решена, эта дизъюнкция считается неправомерной. Такое же требование предъявляется к пониманию всякой дизъюнкции. Это требование интуиционистов может создать затруднения и в случае рассмотрения задач, связанных с конечными множествами. Представим себе, что кто-то, закрыв глаза, достает шар из урны, в к-рой имеются три черных и три белых шара, и тут же бросает этот шар обратно. Если никто не видел этот шар, то мы не имеем возможности узнать, какого он был цвета. Однако вряд ли можно всерьез оспаривать достоверность утверждения, что этот шар был либо черного, либо белого цвета.

Интуиционисты построили свою математику, имеющую интересные своеобразные особенности. Но она оказалась более сложной и громоздкой, чем классич. математика. Положительный вклад интуиционистов в исследование вопросов оснований математики выразился в том, что они еще раз решительным образом подчеркнули различие между конструктивным и неконструктивным в математике, они провели тщательный анализ многих трудностей, с к-рыми столкнулась математика в своем развитии, и тем самым способствовали их преодолению.

Д. Гильберт (D. Hilbert, см. добавления VII-X в [9]) наметил другой путь преодоления трудностей, возникших в основаниях математики на рубеже 19-20 вв. Этот путь, основанный на применении аксиоматич. метода рассмотрения формальных моделей, содержательной математики и на исследовании вопросов непротиворечивости таких моделей надежными финитными средствами, получил в математике название финитизма Гильберта. Признавая ненадежность геометрич. интуиции, Д. Гильберт прежде всего предпринимает тщательный пересмотр евклидовой геометрии, освобождая ее от обращения к интуиции. Результатом такой переработки явились его "Основания геометрии" (1899).

Вопросы непротиворечивости различных теорий по существу рассматривались и до Д. Гильберта. Так, построенная Ф. Клейном (F. Klein, 1871) проективная модель неевклидовой геометрии Лобачевского сводит вопрос о непротиворечивости геометрии Лобачевского к непротиворечивости евклидовой геометрии. Непротиворечивость евклидовой геометрии аналогично можно свести к непротиворечивости анализа, т. е. теории действительных чисел. Однако не видно было, какими средствами можно строить модели анализа и арифметики для доказательства их непротиворечивости. Заслуга Д. Гильберта состоит в том, что он указал прямой путь для исследования этого вопроса. Непротиворечивость данной теории означает, что в ней не может быть получено противоречие, т. е. не может быть доказано нек-рое утверждение Аи его отрицание Д. Гильберт предложил представить рассматриваемую теорию в виде формальной аксиоматич. системы, в к-рой будут выводимы все те и только те утверждения, к-рые являются теоремами нашей теории. Тогда для доказательства непротиворечивости достаточно установить невыводимость в рассматриваемой теории нек-рых утверждений. Таким образом, математич. теория, непротиворечивость к-рой мы хотим доказать, становится предметом изучения нек-рой математич. науки, к-рую Д. Гильберт назвал метаматематикой, или теорией доказательств.

Д. Гильберт писал, что парадоксы теории множеств вызваны не законом исключенного третьего, а "скорее тем, что математики пользуются недопустимыми и бессмысленными образованиями понятий, к-рые в моей теории доказательств исключаются сами собой. ...Отнять у математиков закон исключенного третьего - это то же, что забрать у астрономов телескоп или запретить боксерам использовать кулаки" (см. [9] с. 383). Д. Гильберт предлагает различать "действительные" и "идеальные" предложения классич. математики. Первые имеют содержательный смысл, а вторые не обязаны иметь содержательный смысл. Предложения, соответствующие употреблению актуальной бесконечности, идеальны. Идеальные предложения присоединяются к действительным для того, чтобы простые правила логики были применимы и к рассуждениям о бесконечных множествах. Это существенно упрощает структуру всей теории подобно тому, как при рассмотрении проективной геометрии на плоскости добавляется бесконечно удаленная прямая, пересекающая любые две параллельные прямые в нек-рой точке.

Выдвинутая Д. Гильбертом программа обоснования математики и его энтузиазм вдохновили современников на интенсивную разработку аксиоматического метода. Именно с предпринятой в начале 20 в. Д. Гильбертом и его последователями разработкой теории доказательств на базе развитого в работах Г. Фреге, Дж. Пеано и Б. Рассела логич. языка следует связывать становление М. л. как самостоятельной математич. дисциплины.

Предмет и основные разделы математической логики, связь с другими областями математики. Предмет современной М. л. разнообразен. Прежде всего следует отметить исследование логич. и логико-математич. исчислений, из к-рых основным является классич. исчисление предикатов. Еще в 1930 К. Гёдель (К. Godel) доказал теорему о полноте исчисления предикатов, согласно к-рой множество всех чисто логич. утверждений математики совпадает с множеством всех выводимых в исчислении предикатов формул (см. Гёделя теорема о полноте). Эта теорема показала, что исчисление предикатов является той логич. системой, на базе к-рой можно формализовать математику. На базе исчисления предикатов строятся различные логико-математич. теории (см. Логико-математические исчисления), представляющие собой формализацию содержательных математич. теорий - арифметики, анализа, теории множеств, теории групп и др. Наряду с элементарными теориями рассматриваются также теории высших порядков, в к-рых допускаются также кванторы по предикатам, предикаты от предикатов и т. д. Традиционными вопросами, к-рые исследуются для тех или иных формальных логич. систем, являются исследования структуры выводов в этих системах, выводимость тех или иных формул, вопросы непротиворечивости и полноты рассматриваемых систем.

Доказанная в 1931 Гёделя теорема о неполноте арифметики поколебала оптимистич. надежды Д. Гильберта на полное решение вопросов оснований математики на указанном пути. Согласно этой теореме, если формальная система, содержащая арифметику, непротиворечива, то утверждение о ее непротиворечивости, выразимое в этой системе, не может быть доказано средствами, формализуемыми в ней. Это означает, что с вопросами оснований математики дело обстоит не так просто, как хотелось или казалось Д. Гильберту вначале. Но уже К. Гёдель заметил, что непротиворечивость арифметики можно доказывать, пользуясь достаточно надежными конструктивными средствами, хотя и выходящими за рамки средств, формализуемых в арифметике. Аналогичные доказательства непротиворечивости арифметики были получены Г. Генценом (G. Gentzen, 1936) и П. С. Новиковым (1943).

В результате анализа канторовской теории множеств и связанных с ней парадоксов были построены различные системы аксиоматической теории множеств, в к-рых принимается то или иное ограничение на образование множеств, чтобы исключить возникновение известных антиномий. В этих аксиоматич. системах могут быть развиты довольно обширные разделы математики. Вопрос о непротиворечивости достаточно богатых аксиоматич. систем теории множеств остается открытым. Из наиболее значительных результатов, полученных в аксиоматич. теории множеств, следует отметить результат К. Гёделя о непротиворечивости континуум-гипотезы и выбора аксиомы в системе Бернайса - Гёделя (1939) и результат П. Коэна (P. Cohen, 1963) о независимости этих аксиом от аксиом системы Цермело-Френкеля ZF. Отметим, что эти две системы аксиом 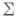и ZF равнонепротиворечивы. Для доказательства своих результатов К. Гёдель ввел важное понятие конструктивного множества (см. Конструктивное по Гёдeлю множество).и показал существование модели системы состоящей из таких множеств. Метод К. Гёделя был использован П. С. Новиковым для доказательства непротиворечивости нек-рых других утверждений дескриптивной теории множеств (1951). Для построения моделей теории множеств ZF, в к-рых выполняются отрицания континуум-гипотезы или аксиомы выбора, П. Коэн ввел так наз. вынуждения метод, к-рый впоследствии был усовершенствован и стал основным методом построения моделей теории множеств, удовлетворяющих тем или иным свойствам.

Одним из наиболее замечательных достижений М. л. явилась разработка понятия общерекурсивной функции и формулировка Чёрча тезиса, утверждающего, что понятие общерекурсивной функции является уточнением интуитивного понятия алгоритма. Из других эквивалентных уточнений понятия алгоритма наибольшее распространение получили понятия Тьюринга машины и нормального алгорифма Маркова. По существу вся математика связана с теми или иными алгоритмами. Но только после уточнения понятия алгоритма появилась возможность обнаружить существование неразрешимых алгоритмических проблем в математике. Неразрешимые алгоритмич. проблемы были обнаружены во многих разделах математики (алгебра, теория чисел, топология, теория вероятностей и др.), причем оказалось, что они могут быть связаны с очень распространенными и фундаментальными понятиями математики. Исследование алгоритмич. проблем в той или иной области математики, как правило, сопровождается проникновением идей и методов М. л. в эту область, что приводит к решению также и других проблем, уже не имеющих алгоритмич. характера.

Разработка точного понятия алгоритма дала возможность уточнить понятие эффективности и развивать на базе такого уточнения конструктивное направление в математике (см. Конструктивная математика), воплотившее в себе нек-рые черты интуиционистского направления, но существенно отличающееся от последнего. Были созданы основы конструктивного анализа, конструктивной топологии, конструктивной теории вероятностей и др.

В самой теории алгоритмов можно выделить исследования в области рекурсивной арифметики, куда входят различные классификации рекурсивных и рекурсивно-перечислимых множеств, степени неразрешимости рекурсивно-перечислимых множеств, исследования сложности записи алгоритмов и сложности алгоритмич. вычислений (по времени и по зоне, см. Алгоритма слож ность). Обширным развивающимся разделом теории алгоритмов является теория нумераций.

Как отмечалось выше, аксиоматич. метод оказал большое влияние на развитие многих разделов математики. Особенно значительным было проникновение этого метода в алгебру. Так, на стыке М. л. и алгебры возникла общая теория алгебраических систем, или моделей теория. Это направление было заложено в работах А. И. Мальцева, А. Тарского (A. Tarski) и их учеников. Здесь можно отметить исследования по элементарным теориям классов моделей, в частности вопросы разрешимости этих теорий, аксиоматизируемость классов моделей, изоморфизм моделей, вопросы категоричности и полноты классов моделей.

Важное место в теории моделей занимает исследование нестандартных моделей арифметики и анализа. Еще на заре развития дифференциального исчисления в работах Г. Лейбница (G. Leibniz) и И. Ньютона (I. Newton) бесконечно малые и бесконечно большие величины рассматривались как числа. Позже появилось понятие переменной величины, и математики отказались от употребления бесконечно малых чисел, модуль к-рых отличен от нуля и меньше любого положительного действительного числа, т. к. их употребление потребовало бы отказа от аксиомы Архимеда. И только через три столетия в результате развития методов М. л. удалось установить, что (нестандартный) анализ с бесконечно малыми и бесконечно большими числами непротиворечив относительно обычного (стандартного) анализа действительных чисел.

Не обошлась без влияния аксиоматич. метода и интуиционистская математика. Так, еще в 1930 А. Рейтинг (A. Heyting) ввел в рассмотрение формальные системы интуиционистской логики высказываний и предикатов (конструктивные исчисления высказываний и предикатов). Позже были введены формальные системы интуиционистского анализа (см., напр., [8]). Многие исследования по интуиционистской логике и математике имеют дело с формальными системами. Подвергались специальному изучению также так наз. промежуточные логики (или суперинтуиционистские), т. е. логики, лежащие между классической и интуиционистской логиками. Понятие реализуемости формул по Клини представляет одну из попыток интерпретировать понятие интуиционистской истинности с точки зрения классич. математики. Однако оказалось, что не всякая реализуемая формула исчисления высказываний выводима в интуиционистском (конструктивном) исчислении высказываний.

Подверглась формализации также и модальная логика. Однако, несмотря на наличие большого числа работ по формальным системам модальной логики и по их семантике (Крипке модели), можно сказать, что здесь происходит процесс накопления пока еще разрозненных фактов.

М. л. имеет большое прикладное значение; с каждым годом растет глубокое проникновение идей и методов М. л. в кибернетику, в вычислительную математику, в структурную лингвистику.

Лит.:[1] Гильберт Д., Б е р н а й с П., Основания математики. Логические исчисления и формализация арифметики, пер. с нем., М., 1979; [2] К л и н и С. К., Введение в метаматематику, пер. с англ., М., 1957; [3] Мендельсон Э., Введение в математическую логику, пер. сангл., 2 изд., М., 1976; [4] Новиков П. С., Элементы математической логики, 2 изд., М., 1973; [5] Е р ш о в Ю. Л., Палютин Е. А., Математическая логика, М., 1979; [6] Ш е н ф и л д Д. Р., Математическая логика, пер. с англ., М., 1975; [7] Н о в и к о в П. С., Конструктивная математическая логика с точки зрения классической, М., 1977; [8] К л и н и С. К., В е с л и Р., Основания интуиционистской математики с точки зрения теории рекурсивных функций, пер. с англ., М., 1978; [9] Гильберт Д., Основания геометрик, пер. с нем., М., 1948; [10] Френкель А.-А., Бар-Хиллел И., Основания теории множеств, пер. с англ., М., 1966; [11] Математика XIX века. Математическая логика. Алгебра. Теория чисел. Теория вероятностей, М., 1978; [12] Mostowski A., Thirty years of foundational studies, Hels., 1965.

См. также лит. при статьях об отдельных разделах М. л.

С. И. Адян.